| Step | Hyp | Ref
| Expression |
|---|
| 1 | | df-nqqs 6446 |
. . . . . 6
            |
| 2 | | id 19 |
. . . . . . . 8
        ![] ]](rbrack.gif)           ![] ]](rbrack.gif)     |
| 3 | 2, 2 | breq12d 3777 |
. . . . . . 7
        ![] ]](rbrack.gif)            ![] ]](rbrack.gif)         ![] ]](rbrack.gif)   
    |
| 4 | 3 | notbid 592 |
. . . . . 6
        ![] ]](rbrack.gif)             ![] ]](rbrack.gif)         ![] ]](rbrack.gif)  
      |
| 5 | | ltsopi 6418 |
. . . . . . . 8
  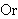  |
| 6 | | ltrelpi 6422 |
. . . . . . . 8
        |
| 7 | 5, 6 | soirri 4719 |
. . . . . . 7
             |
| 8 | | ordpipqqs 6472 |
. . . . . . . . 9
                       
       ![] ]](rbrack.gif)  
      ![] ]](rbrack.gif)  
             |
| 9 | 8 | anidms 377 |
. . . . . . . 8
        
          ![] ]](rbrack.gif)         ![] ]](rbrack.gif)                |
| 10 | | mulcompig 6429 |
. . . . . . . . 9
        
               |
| 11 | 10 | breq1d 3774 |
. . . . . . . 8
        
                             |
| 12 | 9, 11 | bitrd 177 |
. . . . . . 7
        
          ![] ]](rbrack.gif)         ![] ]](rbrack.gif)                |
| 13 | 7, 12 | mtbiri 600 |
. . . . . 6
        
          ![] ]](rbrack.gif)         ![] ]](rbrack.gif)   |
| 14 | 1, 4, 13 | ecoptocl 6193 |
. . . . 5
           |
| 15 | 14 | adantl 262 |
. . . 4
   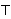            |
| 16 | | breq1 3767 |
. . . . . . . 8
        ![] ]](rbrack.gif)            ![] ]](rbrack.gif)         ![] ]](rbrack.gif)  
        ![] ]](rbrack.gif)    |
| 17 | 16 | anbi1d 438 |
. . . . . . 7
        ![] ]](rbrack.gif)             ![] ]](rbrack.gif)         ![] ]](rbrack.gif)         ![] ]](rbrack.gif)  
      ![] ]](rbrack.gif)             ![] ]](rbrack.gif)         ![] ]](rbrack.gif)         ![] ]](rbrack.gif)     |
| 18 | | breq1 3767 |
. . . . . . 7
        ![] ]](rbrack.gif)            ![] ]](rbrack.gif)         ![] ]](rbrack.gif)  
        ![] ]](rbrack.gif)    |
| 19 | 17, 18 | imbi12d 223 |
. . . . . 6
        ![] ]](rbrack.gif)              ![] ]](rbrack.gif)  
      ![] ]](rbrack.gif)         ![] ]](rbrack.gif)         ![] ]](rbrack.gif)          ![] ]](rbrack.gif)         ![] ]](rbrack.gif)   
          ![] ]](rbrack.gif)         ![] ]](rbrack.gif)         ![] ]](rbrack.gif)            ![] ]](rbrack.gif)     |
| 20 | | breq2 3768 |
. . . . . . . 8
        ![] ]](rbrack.gif)              ![] ]](rbrack.gif)        |
| 21 | | breq1 3767 |
. . . . . . . 8
        ![] ]](rbrack.gif)            ![] ]](rbrack.gif)         ![] ]](rbrack.gif)  
        ![] ]](rbrack.gif)    |
| 22 | 20, 21 | anbi12d 442 |
. . . . . . 7
        ![] ]](rbrack.gif)               ![] ]](rbrack.gif)         ![] ]](rbrack.gif)         ![] ]](rbrack.gif)   
             ![] ]](rbrack.gif)     |
| 23 | 22 | imbi1d 220 |
. . . . . 6
        ![] ]](rbrack.gif)                ![] ]](rbrack.gif)         ![] ]](rbrack.gif)  
      ![] ]](rbrack.gif)            ![] ]](rbrack.gif)                  ![] ]](rbrack.gif)            ![] ]](rbrack.gif)     |
| 24 | | breq2 3768 |
. . . . . . . 8
        ![] ]](rbrack.gif)              ![] ]](rbrack.gif)        |
| 25 | 24 | anbi2d 437 |
. . . . . . 7
        ![] ]](rbrack.gif)                   ![] ]](rbrack.gif)         
     |
| 26 | | breq2 3768 |
. . . . . . 7
        ![] ]](rbrack.gif)              ![] ]](rbrack.gif)        |
| 27 | 25, 26 | imbi12d 223 |
. . . . . 6
        ![] ]](rbrack.gif)          
         ![] ]](rbrack.gif)            ![] ]](rbrack.gif)              
      |
| 28 | | ordpipqqs 6472 |
. . . . . . . . . . . . . . . 16
                       
       ![] ]](rbrack.gif)  
      ![] ]](rbrack.gif)                |
| 29 | 28 | 3adant3 924 |
. . . . . . . . . . . . . . 15
                                 
       ![] ]](rbrack.gif)  
      ![] ]](rbrack.gif)                |
| 30 | | simp1l 928 |
. . . . . . . . . . . . . . . . 17
                                 
    |
| 31 | | simp2r 931 |
. . . . . . . . . . . . . . . . 17
                                 
    |
| 32 | | mulclpi 6426 |
. . . . . . . . . . . . . . . . 17
        
           |
| 33 | 30, 31, 32 | syl2anc 391 |
. . . . . . . . . . . . . . . 16
                                 
        |
| 34 | | simp1r 929 |
. . . . . . . . . . . . . . . . 17
                                 
    |
| 35 | | simp2l 930 |
. . . . . . . . . . . . . . . . 17
                                 
    |
| 36 | | mulclpi 6426 |
. . . . . . . . . . . . . . . . 17
        
           |
| 37 | 34, 35, 36 | syl2anc 391 |
. . . . . . . . . . . . . . . 16
                                 
        |
| 38 | | simp3r 933 |
. . . . . . . . . . . . . . . . 17
                                 
    |
| 39 | | mulclpi 6426 |
. . . . . . . . . . . . . . . . 17
        
           |
| 40 | 35, 38, 39 | syl2anc 391 |
. . . . . . . . . . . . . . . 16
                                 
        |
| 41 | | ltmpig 6437 |
. . . . . . . . . . . . . . . 16
                                                      
               |
| 42 | 33, 37, 40, 41 | syl3anc 1135 |
. . . . . . . . . . . . . . 15
                                 
                                          |
| 43 | 29, 42 | bitrd 177 |
. . . . . . . . . . . . . 14
                                 
       ![] ]](rbrack.gif)  
      ![] ]](rbrack.gif)                                |
| 44 | 43 | biimpa 280 |
. . . . . . . . . . . . 13
        
   
       
             
      ![] ]](rbrack.gif)         ![] ]](rbrack.gif)                 
              |
| 45 | 44 | adantrr 448 |
. . . . . . . . . . . 12
        
   
       
             
       ![] ]](rbrack.gif)  
      ![] ]](rbrack.gif)         ![] ]](rbrack.gif)         ![] ]](rbrack.gif)                                 |
| 46 | | mulcompig 6429 |
. . . . . . . . . . . . . 14
                                                |
| 47 | 40, 37, 46 | syl2anc 391 |
. . . . . . . . . . . . 13
                                 
                            |
| 48 | 47 | adantr 261 |
. . . . . . . . . . . 12
        
   
       
             
       ![] ]](rbrack.gif)  
      ![] ]](rbrack.gif)         ![] ]](rbrack.gif)         ![] ]](rbrack.gif)                                 |
| 49 | 45, 48 | breqtrd 3788 |
. . . . . . . . . . 11
        
   
       
             
       ![] ]](rbrack.gif)  
      ![] ]](rbrack.gif)         ![] ]](rbrack.gif)         ![] ]](rbrack.gif)                                 |
| 50 | | ordpipqqs 6472 |
. . . . . . . . . . . . . . 15
                       
       ![] ]](rbrack.gif)  
      ![] ]](rbrack.gif)                |
| 51 | 50 | 3adant1 922 |
. . . . . . . . . . . . . 14
                                 
       ![] ]](rbrack.gif)  
      ![] ]](rbrack.gif)                |
| 52 | | simp3l 932 |
. . . . . . . . . . . . . . . 16
                                 
    |
| 53 | | mulclpi 6426 |
. . . . . . . . . . . . . . . 16
        
           |
| 54 | 31, 52, 53 | syl2anc 391 |
. . . . . . . . . . . . . . 15
                                 
        |
| 55 | | ltmpig 6437 |
. . . . . . . . . . . . . . 15
                                                      
               |
| 56 | 40, 54, 37, 55 | syl3anc 1135 |
. . . . . . . . . . . . . 14
                                 
                                          |
| 57 | 51, 56 | bitrd 177 |
. . . . . . . . . . . . 13
                                 
       ![] ]](rbrack.gif)  
      ![] ]](rbrack.gif)                                |
| 58 | 57 | biimpa 280 |
. . . . . . . . . . . 12
        
   
       
             
      ![] ]](rbrack.gif)         ![] ]](rbrack.gif)                 
              |
| 59 | 58 | adantrl 447 |
. . . . . . . . . . 11
        
   
       
             
       ![] ]](rbrack.gif)  
      ![] ]](rbrack.gif)         ![] ]](rbrack.gif)         ![] ]](rbrack.gif)                                 |
| 60 | 5, 6 | sotri 4720 |
. . . . . . . . . . 11
                
                           
                                           |
| 61 | 49, 59, 60 | syl2anc 391 |
. . . . . . . . . 10
        
   
       
             
       ![] ]](rbrack.gif)  
      ![] ]](rbrack.gif)         ![] ]](rbrack.gif)         ![] ]](rbrack.gif)                                 |
| 62 | | mulcompig 6429 |
. . . . . . . . . . . . . . 15
        
               |
| 63 | 62 | adantl 262 |
. . . . . . . . . . . . . 14
        
   
       
             
                       |
| 64 | | mulasspig 6430 |
. . . . . . . . . . . . . . 15
        
                           |
| 65 | 64 | adantl 262 |
. . . . . . . . . . . . . 14
        
   
       
             
        
                          |
| 66 | | mulclpi 6426 |
. . . . . . . . . . . . . . 15
        
           |
| 67 | 66 | adantl 262 |
. . . . . . . . . . . . . 14
        
   
       
             
                   |
| 68 | 35, 31, 30, 63, 65, 38, 67 | caov411d 5686 |
. . . . . . . . . . . . 13
                                 
                            |
| 69 | 63, 33, 40 | caovcomd 5657 |
. . . . . . . . . . . . 13
                                 
                            |
| 70 | 68, 69 | eqtrd 2072 |
. . . . . . . . . . . 12
                                 
                            |
| 71 | 35, 31, 34, 63, 65, 52, 67 | caov4d 5685 |
. . . . . . . . . . . . 13
                                 
                            |
| 72 | 63, 35, 34 | caovcomd 5657 |
. . . . . . . . . . . . . 14
                                 
            |
| 73 | 72 | oveq1d 5527 |
. . . . . . . . . . . . 13
                                 
                            |
| 74 | 71, 73 | eqtrd 2072 |
. . . . . . . . . . . 12
                                 
                            |
| 75 | 70, 74 | breq12d 3777 |
. . . . . . . . . . 11
                                 
                                                          |
| 76 | 75 | adantr 261 |
. . . . . . . . . 10
        
   
       
             
       ![] ]](rbrack.gif)  
      ![] ]](rbrack.gif)         ![] ]](rbrack.gif)         ![] ]](rbrack.gif)                   
             
                             |
| 77 | 61, 76 | mpbird 156 |
. . . . . . . . 9
        
   
       
             
       ![] ]](rbrack.gif)  
      ![] ]](rbrack.gif)         ![] ]](rbrack.gif)         ![] ]](rbrack.gif)                                 |
| 78 | | mulclpi 6426 |
. . . . . . . . . . . 12
        
           |
| 79 | 30, 38, 78 | syl2anc 391 |
. . . . . . . . . . 11
                                 
        |
| 80 | | mulclpi 6426 |
. . . . . . . . . . . 12
        
           |
| 81 | 34, 52, 80 | syl2anc 391 |
. . . . . . . . . . 11
                                 
        |
| 82 | | mulclpi 6426 |
. . . . . . . . . . . 12
        
           |
| 83 | 35, 31, 82 | syl2anc 391 |
. . . . . . . . . . 11
                                 
        |
| 84 | | ltmpig 6437 |
. . . . . . . . . . 11
                                                      
               |
| 85 | 79, 81, 83, 84 | syl3anc 1135 |
. . . . . . . . . 10
                                 
                                          |
| 86 | 85 | adantr 261 |
. . . . . . . . 9
        
   
       
             
       ![] ]](rbrack.gif)  
      ![] ]](rbrack.gif)         ![] ]](rbrack.gif)         ![] ]](rbrack.gif)                 
                             |
| 87 | 77, 86 | mpbird 156 |
. . . . . . . 8
        
   
       
             
       ![] ]](rbrack.gif)  
      ![] ]](rbrack.gif)         ![] ]](rbrack.gif)         ![] ]](rbrack.gif)                 |
| 88 | | ordpipqqs 6472 |
. . . . . . . . . 10
                       
       ![] ]](rbrack.gif)  
      ![] ]](rbrack.gif)                |
| 89 | 88 | 3adant2 923 |
. . . . . . . . 9
                                 
       ![] ]](rbrack.gif)  
      ![] ]](rbrack.gif)                |
| 90 | 89 | adantr 261 |
. . . . . . . 8
        
   
       
             
       ![] ]](rbrack.gif)  
      ![] ]](rbrack.gif)         ![] ]](rbrack.gif)         ![] ]](rbrack.gif)            ![] ]](rbrack.gif)         ![] ]](rbrack.gif)                |
| 91 | 87, 90 | mpbird 156 |
. . . . . . 7
        
   
       
             
       ![] ]](rbrack.gif)  
      ![] ]](rbrack.gif)         ![] ]](rbrack.gif)         ![] ]](rbrack.gif)           ![] ]](rbrack.gif)         ![] ]](rbrack.gif)   |
| 92 | 91 | ex 108 |
. . . . . 6
                                 
        ![] ]](rbrack.gif)         ![] ]](rbrack.gif)         ![] ]](rbrack.gif)         ![] ]](rbrack.gif)          ![] ]](rbrack.gif)         ![] ]](rbrack.gif)    |
| 93 | 1, 19, 23, 27, 92 | 3ecoptocl 6195 |
. . . . 5
        
             
         |
| 94 | 93 | adantl 262 |
. . . 4
   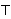                           
     |
| 95 | 15, 94 | ispod 4041 |
. . 3
  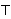   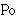   |
| 96 | | nqtri3or 6494 |
. . . 4
        
        
   
    |
| 97 | 96 | adantl 262 |
. . 3
   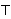                  
   
    |
| 98 | 95, 97 | issod 4056 |
. 2
  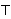   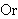   |
| 99 | 98 | trud 1252 |
1
    |