Description: Axiom of Existence. One
of the equality and substitution axioms of
predicate calculus with equality. One thing this axiom tells us is that
at least one thing exists (although ax-4 1400
and possibly others also tell
us that, i.e. they are not valid in the empty domain of a "free
logic").
In this form (not requiring that 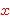 and and  be distinct) it was used
in an axiom system of Tarski (see Axiom B7' in footnote 1 of
[KalishMontague] p. 81.) Another
name for this theorem is a9e 1586, which
has additional remarks. (Contributed by Mario Carneiro,
31-Jan-2015.)
be distinct) it was used
in an axiom system of Tarski (see Axiom B7' in footnote 1 of
[KalishMontague] p. 81.) Another
name for this theorem is a9e 1586, which
has additional remarks. (Contributed by Mario Carneiro,
31-Jan-2015.) |