Description: Axiom of Specialization.
A quantified wff implies the wff without a
quantifier (i.e. an instance, or special case, of the generalized wff).
In other words if something is true for all  , it is true for any
specific , it is true for any
specific  (that
would typically occur as a free variable in the wff
substituted for (that
would typically occur as a free variable in the wff
substituted for  ). (A free variable is one that does not occur in
the scope of a quantifier: ). (A free variable is one that does not occur in
the scope of a quantifier:  and and  are both
free in are both
free in  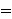  ,
but only ,
but only  is free
in is free
in 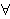   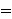  .) Axiom
scheme C5' in [Megill]
p. 448 (p. 16 of the preprint). Also appears as Axiom B5 of [Tarski]
p. 67 (under his system S2, defined in the last paragraph on p. 77). .) Axiom
scheme C5' in [Megill]
p. 448 (p. 16 of the preprint). Also appears as Axiom B5 of [Tarski]
p. 67 (under his system S2, defined in the last paragraph on p. 77).
Note that the converse of this axiom does not hold in general, but a
weaker inference form of the converse holds and is expressed as rule
ax-gen 1338. Conditional forms of the converse are given
by ax-12 1402,
ax-16 1695, and ax-17 1419.
Unlike the more general textbook Axiom of Specialization, we cannot choose
a variable different from  for the special case. For use, that
requires the assistance of equality axioms, and we deal with it later
after we introduce the definition of proper substitution - see stdpc4 1658. for the special case. For use, that
requires the assistance of equality axioms, and we deal with it later
after we introduce the definition of proper substitution - see stdpc4 1658.
(Contributed by NM, 5-Aug-1993.) |