Description: Bound-variable hypothesis
builder for  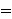  . This theorem tells us
that any variable, including . This theorem tells us
that any variable, including  , is effectively not free in , is effectively not free in
 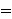  , even though , even though  is technically free according to the
traditional definition of free variable. (The proof uses only ax-5 1336,
ax-8 1395, ax-12 1402, and ax-gen 1338. This shows that this can be proved
without ax-9 1424, even though the theorem equid 1589 cannot be. A shorter
proof using ax-9 1424 is obtainable from equid 1589 and hbth 1352.) (Contributed
by NM, 13-Jan-2011.) (Proof shortened by Wolf Lammen,
23-Mar-2014.) is technically free according to the
traditional definition of free variable. (The proof uses only ax-5 1336,
ax-8 1395, ax-12 1402, and ax-gen 1338. This shows that this can be proved
without ax-9 1424, even though the theorem equid 1589 cannot be. A shorter
proof using ax-9 1424 is obtainable from equid 1589 and hbth 1352.) (Contributed
by NM, 13-Jan-2011.) (Proof shortened by Wolf Lammen,
23-Mar-2014.) |