Description: Axiom of Quantifier
Introduction. One of the equality and substitution
axioms of predicate calculus with equality. Informally, it says that
whenever  is
distinct from is
distinct from  and and  , and , and  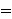  is
true,
then is
true,
then  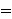  quantified with quantified with  is also true. In other words, is also true. In other words,  is irrelevant to the truth of
is irrelevant to the truth of  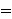  . Axiom scheme C9' in [Megill]
p. 448 (p. 16 of the preprint). It apparently does not otherwise appear
in the literature but is easily proved from textbook predicate calculus by
cases. . Axiom scheme C9' in [Megill]
p. 448 (p. 16 of the preprint). It apparently does not otherwise appear
in the literature but is easily proved from textbook predicate calculus by
cases.
This axiom has been modified from the original ax-12 1402 for compatibility
with intuitionistic logic. (Contributed by Mario Carneiro,
31-Jan-2015.) |