Description: Define the not-free
predicate for wffs. This is read " is not free
in is not free
in  ".
Not-free means that the value of ".
Not-free means that the value of  cannot affect the
value of cannot affect the
value of  ,
e.g., any occurrence of ,
e.g., any occurrence of  in in  is effectively
bound by a "for all" or something that expands to one (such as
"there
exists"). In particular, substitution for a variable not free in a
wff
does not affect its value (sbf 1660). An example of where this is used is
stdpc5 1476. See nf2 1558 for an alternative definition which
does not involve
nested quantifiers on the same variable.
is effectively
bound by a "for all" or something that expands to one (such as
"there
exists"). In particular, substitution for a variable not free in a
wff
does not affect its value (sbf 1660). An example of where this is used is
stdpc5 1476. See nf2 1558 for an alternative definition which
does not involve
nested quantifiers on the same variable.
Not-free is a commonly used constraint, so it is useful to have a notation
for it. Surprisingly, there is no common formal notation for it, so here
we devise one. Our definition lets us work with the not-free notion
within the logic itself rather than as a metalogical side condition.
To be precise, our definition really means "effectively not
free," because
it is slightly less restrictive than the usual textbook definition for
not-free (which only considers syntactic freedom). For example,  is
effectively not free in the bare expression is
effectively not free in the bare expression  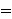  , even
though , even
though  would be considered free in the usual textbook definition, because the
value of
would be considered free in the usual textbook definition, because the
value of  in the
expression in the
expression  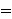  cannot affect the truth of the
expression (and thus substitution will not change the result).
(Contributed by Mario Carneiro, 11-Aug-2016.) cannot affect the truth of the
expression (and thus substitution will not change the result).
(Contributed by Mario Carneiro, 11-Aug-2016.) |