Theorem caucvgprprlemopl 6795

Description: Lemma for caucvgprpr 6810. The lower cut of the putative limit is open. (Contributed by Jim Kingdon, 21-Dec-2020.)

Hypotheses

Ref	Expression
caucvgprpr.f	|- ( ph -> F : N. --> P. )
caucvgprpr.cau	|- ( ph -> A. n e. N. A. k e. N. ( n <N k -> ( ( F ` n ) <P ( ( F ` k ) +P. <. { l | l <Q ( *Q ` [ <. n , 1o >. ] ~Q ) } , { u | ( *Q ` [ <. n , 1o >. ] ~Q ) <Q u } >. ) /\ ( F ` k ) <P ( ( F ` n ) +P. <. { l | l <Q ( *Q ` [ <. n , 1o >. ] ~Q ) } , { u | ( *Q ` [ <. n , 1o >. ] ~Q ) <Q u } >. ) ) ) )
caucvgprpr.bnd	|- ( ph -> A. m e. N. A <P ( F ` m ) )
caucvgprpr.lim	|- L = <. { l e. Q. | E. r e. N. <. { p | p <Q ( l +Q ( *Q ` [ <. r , 1o >. ] ~Q ) ) } , { q | ( l +Q ( *Q ` [ <. r , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` r ) } , { u e. Q. | E. r e. N. ( ( F ` r ) +P. <. { p | p <Q ( *Q ` [ <. r , 1o >. ] ~Q ) } , { q | ( *Q ` [ <. r , 1o >. ] ~Q ) <Q q } >. ) <P <. { p | p <Q u } , { q | u <Q q } >. } >.

Assertion

Ref	Expression
caucvgprprlemopl	|- ( ( ph /\ s e. ( 1st ` L ) ) -> E. t e. Q. ( s <Q t /\ t e. ( 1st ` L ) ) )

Distinct variable groups:   A, m   m, F   F, l, t, r   u, F, t   t, L   p, l, q, r, s, t   u, p, q, r, s   ph, r, t

Allowed substitution hints:   ph( u, k, m, n, s, q, p, l)   A( u, t, k, n, s, r, q, p, l)   F( k, n, s, q, p)   L( u, k, m, n, s, r, q, p, l)

Proof of Theorem caucvgprprlemopl

Dummy variables a b are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		caucvgprpr.lim	. . . . 5 |- L = <. { l e. Q. | E. r e. N. <. { p | p <Q ( l +Q ( *Q ` [ <. r , 1o >. ] ~Q ) ) } , { q | ( l +Q ( *Q ` [ <. r , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` r ) } , { u e. Q. | E. r e. N. ( ( F ` r ) +P. <. { p | p <Q ( *Q ` [ <. r , 1o >. ] ~Q ) } , { q | ( *Q ` [ <. r , 1o >. ] ~Q ) <Q q } >. ) <P <. { p | p <Q u } , { q | u <Q q } >. } >.
2	1	caucvgprprlemell 6783	. . . 4 |- ( s e. ( 1st ` L ) <-> ( s e. Q. /\ E. b e. N. <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) )
3	2	simprbi 260	. . 3 |- ( s e. ( 1st ` L ) -> E. b e. N. <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) )
4	3	adantl 262	. 2 |- ( ( ph /\ s e. ( 1st ` L ) ) -> E. b e. N. <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) )
5		caucvgprpr.f	. . . . . . 7 |- ( ph -> F : N. --> P. )
6	5	ad2antrr 457	. . . . . 6 |- ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) -> F : N. --> P. )
7		simprl 483	. . . . . 6 |- ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) -> b e. N. )
8	6, 7	ffvelrnd 5303	. . . . 5 |- ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) -> ( F ` b ) e. P. )
9		prop 6573	. . . . 5 |- ( ( F ` b ) e. P. -> <. ( 1st ` ( F ` b ) ) , ( 2nd ` ( F ` b ) ) >. e. P. )
10	8, 9	syl 14	. . . 4 |- ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) -> <. ( 1st ` ( F ` b ) ) , ( 2nd ` ( F ` b ) ) >. e. P. )
11		simprr 484	. . . . 5 |- ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) -> <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) )
12	1	caucvgprprlemell 6783	. . . . . . . . 9 |- ( s e. ( 1st ` L ) <-> ( s e. Q. /\ E. r e. N. <. { p | p <Q ( s +Q ( *Q ` [ <. r , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. r , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` r ) ) )
13	12	simplbi 259	. . . . . . . 8 |- ( s e. ( 1st ` L ) -> s e. Q. )
14	13	ad2antlr 458	. . . . . . 7 |- ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) -> s e. Q. )
15		nnnq 6520	. . . . . . . . 9 |- ( b e. N. -> [ <. b , 1o >. ] ~Q e. Q. )
16		recclnq 6490	. . . . . . . . 9 |- ( [ <. b , 1o >. ] ~Q e. Q. -> ( *Q ` [ <. b , 1o >. ] ~Q ) e. Q. )
17	15, 16	syl 14	. . . . . . . 8 |- ( b e. N. -> ( *Q ` [ <. b , 1o >. ] ~Q ) e. Q. )
18	17	ad2antrl 459	. . . . . . 7 |- ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) -> ( *Q ` [ <. b , 1o >. ] ~Q ) e. Q. )
19		addclnq 6473	. . . . . . 7 |- ( ( s e. Q. /\ ( *Q ` [ <. b , 1o >. ] ~Q ) e. Q. ) -> ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) e. Q. )
20	14, 18, 19	syl2anc 391	. . . . . 6 |- ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) -> ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) e. Q. )
21		nqprl 6649	. . . . . 6 |- ( ( ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) e. Q. /\ ( F ` b ) e. P. ) -> ( ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) e. ( 1st ` ( F ` b ) ) <-> <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) )
22	20, 8, 21	syl2anc 391	. . . . 5 |- ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) -> ( ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) e. ( 1st ` ( F ` b ) ) <-> <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) )
23	11, 22	mpbird 156	. . . 4 |- ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) -> ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) e. ( 1st ` ( F ` b ) ) )
24		prnmaxl 6586	. . . 4 |- ( ( <. ( 1st ` ( F ` b ) ) , ( 2nd ` ( F ` b ) ) >. e. P. /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) e. ( 1st ` ( F ` b ) ) ) -> E. a e. ( 1st ` ( F ` b ) ) ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a )
25	10, 23, 24	syl2anc 391	. . 3 |- ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) -> E. a e. ( 1st ` ( F ` b ) ) ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a )
26	18	adantr 261	. . . . . . . 8 |- ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) -> ( *Q ` [ <. b , 1o >. ] ~Q ) e. Q. )
27	14	adantr 261	. . . . . . . 8 |- ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) -> s e. Q. )
28		ltaddnq 6505	. . . . . . . 8 |- ( ( ( *Q ` [ <. b , 1o >. ] ~Q ) e. Q. /\ s e. Q. ) -> ( *Q ` [ <. b , 1o >. ] ~Q ) <Q ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q s ) )
29	26, 27, 28	syl2anc 391	. . . . . . 7 |- ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) -> ( *Q ` [ <. b , 1o >. ] ~Q ) <Q ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q s ) )
30		addcomnqg 6479	. . . . . . . 8 |- ( ( ( *Q ` [ <. b , 1o >. ] ~Q ) e. Q. /\ s e. Q. ) -> ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q s ) = ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) )
31	26, 27, 30	syl2anc 391	. . . . . . 7 |- ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) -> ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q s ) = ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) )
32	29, 31	breqtrd 3788	. . . . . 6 |- ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) -> ( *Q ` [ <. b , 1o >. ] ~Q ) <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) )
33		simprr 484	. . . . . 6 |- ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) -> ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a )
34		ltsonq 6496	. . . . . . 7 |- <Q Or Q.
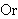35		ltrelnq 6463	. . . . . . 7 |- <Q C_ ( Q. X. Q. )
36	34, 35	sotri 4720	. . . . . 6 |- ( ( ( *Q ` [ <. b , 1o >. ] ~Q ) <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) -> ( *Q ` [ <. b , 1o >. ] ~Q ) <Q a )
37	32, 33, 36	syl2anc 391	. . . . 5 |- ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) -> ( *Q ` [ <. b , 1o >. ] ~Q ) <Q a )
38	10	adantr 261	. . . . . . 7 |- ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) -> <. ( 1st ` ( F ` b ) ) , ( 2nd ` ( F ` b ) ) >. e. P. )
39		simprl 483	. . . . . . 7 |- ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) -> a e. ( 1st ` ( F ` b ) ) )
40		elprnql 6579	. . . . . . 7 |- ( ( <. ( 1st ` ( F ` b ) ) , ( 2nd ` ( F ` b ) ) >. e. P. /\ a e. ( 1st ` ( F ` b ) ) ) -> a e. Q. )
41	38, 39, 40	syl2anc 391	. . . . . 6 |- ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) -> a e. Q. )
42		ltexnqq 6506	. . . . . 6 |- ( ( ( *Q ` [ <. b , 1o >. ] ~Q ) e. Q. /\ a e. Q. ) -> ( ( *Q ` [ <. b , 1o >. ] ~Q ) <Q a <-> E. t e. Q. ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = a ) )
43	26, 41, 42	syl2anc 391	. . . . 5 |- ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) -> ( ( *Q ` [ <. b , 1o >. ] ~Q ) <Q a <-> E. t e. Q. ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = a ) )
44	37, 43	mpbid 135	. . . 4 |- ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) -> E. t e. Q. ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = a )
45	27	ad2antrr 457	. . . . . . . . . . 11 |- ( ( ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) /\ t e. Q. ) /\ ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = a ) -> s e. Q. )
46	26	ad2antrr 457	. . . . . . . . . . 11 |- ( ( ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) /\ t e. Q. ) /\ ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = a ) -> ( *Q ` [ <. b , 1o >. ] ~Q ) e. Q. )
47		addcomnqg 6479	. . . . . . . . . . 11 |- ( ( s e. Q. /\ ( *Q ` [ <. b , 1o >. ] ~Q ) e. Q. ) -> ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) = ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q s ) )
48	45, 46, 47	syl2anc 391	. . . . . . . . . 10 |- ( ( ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) /\ t e. Q. ) /\ ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = a ) -> ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) = ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q s ) )
49	33	ad2antrr 457	. . . . . . . . . 10 |- ( ( ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) /\ t e. Q. ) /\ ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = a ) -> ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a )
50	48, 49	eqbrtrrd 3786	. . . . . . . . 9 |- ( ( ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) /\ t e. Q. ) /\ ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = a ) -> ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q s ) <Q a )
51		simpr 103	. . . . . . . . 9 |- ( ( ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) /\ t e. Q. ) /\ ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = a ) -> ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = a )
52	50, 51	breqtrrd 3790	. . . . . . . 8 |- ( ( ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) /\ t e. Q. ) /\ ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = a ) -> ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q s ) <Q ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) )
53		simplr 482	. . . . . . . . 9 |- ( ( ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) /\ t e. Q. ) /\ ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = a ) -> t e. Q. )
54		ltanqg 6498	. . . . . . . . 9 |- ( ( s e. Q. /\ t e. Q. /\ ( *Q ` [ <. b , 1o >. ] ~Q ) e. Q. ) -> ( s <Q t <-> ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q s ) <Q ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) ) )
55	45, 53, 46, 54	syl3anc 1135	. . . . . . . 8 |- ( ( ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) /\ t e. Q. ) /\ ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = a ) -> ( s <Q t <-> ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q s ) <Q ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) ) )
56	52, 55	mpbird 156	. . . . . . 7 |- ( ( ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) /\ t e. Q. ) /\ ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = a ) -> s <Q t )
57	7	ad3antrrr 461	. . . . . . . . 9 |- ( ( ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) /\ t e. Q. ) /\ ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = a ) -> b e. N. )
58		addcomnqg 6479	. . . . . . . . . . . . 13 |- ( ( ( *Q ` [ <. b , 1o >. ] ~Q ) e. Q. /\ t e. Q. ) -> ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = ( t +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) )
59	46, 53, 58	syl2anc 391	. . . . . . . . . . . 12 |- ( ( ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) /\ t e. Q. ) /\ ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = a ) -> ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = ( t +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) )
60	59, 51	eqtr3d 2074	. . . . . . . . . . 11 |- ( ( ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) /\ t e. Q. ) /\ ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = a ) -> ( t +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) = a )
61	39	ad2antrr 457	. . . . . . . . . . 11 |- ( ( ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) /\ t e. Q. ) /\ ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = a ) -> a e. ( 1st ` ( F ` b ) ) )
62	60, 61	eqeltrd 2114	. . . . . . . . . 10 |- ( ( ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) /\ t e. Q. ) /\ ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = a ) -> ( t +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) e. ( 1st ` ( F ` b ) ) )
63		addclnq 6473	. . . . . . . . . . . 12 |- ( ( t e. Q. /\ ( *Q ` [ <. b , 1o >. ] ~Q ) e. Q. ) -> ( t +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) e. Q. )
64	53, 46, 63	syl2anc 391	. . . . . . . . . . 11 |- ( ( ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) /\ t e. Q. ) /\ ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = a ) -> ( t +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) e. Q. )
65	8	ad3antrrr 461	. . . . . . . . . . 11 |- ( ( ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) /\ t e. Q. ) /\ ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = a ) -> ( F ` b ) e. P. )
66		nqprl 6649	. . . . . . . . . . 11 |- ( ( ( t +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) e. Q. /\ ( F ` b ) e. P. ) -> ( ( t +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) e. ( 1st ` ( F ` b ) ) <-> <. { p | p <Q ( t +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( t +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) )
67	64, 65, 66	syl2anc 391	. . . . . . . . . 10 |- ( ( ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) /\ t e. Q. ) /\ ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = a ) -> ( ( t +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) e. ( 1st ` ( F ` b ) ) <-> <. { p | p <Q ( t +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( t +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) )
68	62, 67	mpbid 135	. . . . . . . . 9 |- ( ( ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) /\ t e. Q. ) /\ ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = a ) -> <. { p | p <Q ( t +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( t +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) )
69		opeq1 3549	. . . . . . . . . . . . . . . . 17 |- ( r = b -> <. r , 1o >. = <. b , 1o >. )
70	69	eceq1d 6142	. . . . . . . . . . . . . . . 16 |- ( r = b -> [ <. r , 1o >. ] ~Q = [ <. b , 1o >. ] ~Q )
71	70	fveq2d 5182	. . . . . . . . . . . . . . 15 |- ( r = b -> ( *Q ` [ <. r , 1o >. ] ~Q ) = ( *Q ` [ <. b , 1o >. ] ~Q ) )
72	71	oveq2d 5528	. . . . . . . . . . . . . 14 |- ( r = b -> ( t +Q ( *Q ` [ <. r , 1o >. ] ~Q ) ) = ( t +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) )
73	72	breq2d 3776	. . . . . . . . . . . . 13 |- ( r = b -> ( p <Q ( t +Q ( *Q ` [ <. r , 1o >. ] ~Q ) ) <-> p <Q ( t +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) ) )
74	73	abbidv 2155	. . . . . . . . . . . 12 |- ( r = b -> { p | p <Q ( t +Q ( *Q ` [ <. r , 1o >. ] ~Q ) ) } = { p | p <Q ( t +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } )
75	72	breq1d 3774	. . . . . . . . . . . . 13 |- ( r = b -> ( ( t +Q ( *Q ` [ <. r , 1o >. ] ~Q ) ) <Q q <-> ( t +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q ) )
76	75	abbidv 2155	. . . . . . . . . . . 12 |- ( r = b -> { q | ( t +Q ( *Q ` [ <. r , 1o >. ] ~Q ) ) <Q q } = { q | ( t +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } )
77	74, 76	opeq12d 3557	. . . . . . . . . . 11 |- ( r = b -> <. { p | p <Q ( t +Q ( *Q ` [ <. r , 1o >. ] ~Q ) ) } , { q | ( t +Q ( *Q ` [ <. r , 1o >. ] ~Q ) ) <Q q } >. = <. { p | p <Q ( t +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( t +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. )
78		fveq2 5178	. . . . . . . . . . 11 |- ( r = b -> ( F ` r ) = ( F ` b ) )
79	77, 78	breq12d 3777	. . . . . . . . . 10 |- ( r = b -> ( <. { p | p <Q ( t +Q ( *Q ` [ <. r , 1o >. ] ~Q ) ) } , { q | ( t +Q ( *Q ` [ <. r , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` r ) <-> <. { p | p <Q ( t +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( t +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) )
80	79	rspcev 2656	. . . . . . . . 9 |- ( ( b e. N. /\ <. { p | p <Q ( t +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( t +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) -> E. r e. N. <. { p | p <Q ( t +Q ( *Q ` [ <. r , 1o >. ] ~Q ) ) } , { q | ( t +Q ( *Q ` [ <. r , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` r ) )
81	57, 68, 80	syl2anc 391	. . . . . . . 8 |- ( ( ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) /\ t e. Q. ) /\ ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = a ) -> E. r e. N. <. { p | p <Q ( t +Q ( *Q ` [ <. r , 1o >. ] ~Q ) ) } , { q | ( t +Q ( *Q ` [ <. r , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` r ) )
82	1	caucvgprprlemell 6783	. . . . . . . 8 |- ( t e. ( 1st ` L ) <-> ( t e. Q. /\ E. r e. N. <. { p | p <Q ( t +Q ( *Q ` [ <. r , 1o >. ] ~Q ) ) } , { q | ( t +Q ( *Q ` [ <. r , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` r ) ) )
83	53, 81, 82	sylanbrc 394	. . . . . . 7 |- ( ( ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) /\ t e. Q. ) /\ ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = a ) -> t e. ( 1st ` L ) )
84	56, 83	jca 290	. . . . . 6 |- ( ( ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) /\ t e. Q. ) /\ ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = a ) -> ( s <Q t /\ t e. ( 1st ` L ) ) )
85	84	ex 108	. . . . 5 |- ( ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) /\ t e. Q. ) -> ( ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = a -> ( s <Q t /\ t e. ( 1st ` L ) ) ) )
86	85	reximdva 2421	. . . 4 |- ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) -> ( E. t e. Q. ( ( *Q ` [ <. b , 1o >. ] ~Q ) +Q t ) = a -> E. t e. Q. ( s <Q t /\ t e. ( 1st ` L ) ) ) )
87	44, 86	mpd 13	. . 3 |- ( ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) /\ ( a e. ( 1st ` ( F ` b ) ) /\ ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q a ) ) -> E. t e. Q. ( s <Q t /\ t e. ( 1st ` L ) ) )
88	25, 87	rexlimddv 2437	. 2 |- ( ( ( ph /\ s e. ( 1st ` L ) ) /\ ( b e. N. /\ <. { p | p <Q ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) } , { q | ( s +Q ( *Q ` [ <. b , 1o >. ] ~Q ) ) <Q q } >. <P ( F ` b ) ) ) -> E. t e. Q. ( s <Q t /\ t e. ( 1st ` L ) ) )
89	4, 88	rexlimddv 2437	1 |- ( ( ph /\ s e. ( 1st ` L ) ) -> E. t e. Q. ( s <Q t /\ t e. ( 1st ` L ) ) )

Syntax hints:   -> wi 4   /\ wa 97   <-> wb 98   = wceq 1243   e. wcel 1393   {cab 2026   A.wral 2306   E.wrex 2307   {crab 2310   <.cop 3378   class class class wbr 3764   -->wf 4898   ` cfv 4902  (class class class)co 5512   1stc1st 5765   2ndc2nd 5766   1oc1o 5994   [cec 6104   N.cnpi 6370   <N clti 6373   ~Q ceq 6377   Q.cnq 6378   +Q cplq 6380   *Qcrq 6382   <Q cltq 6383   P.cnp 6389   +P. cpp 6391   <P cltp 6393

This theorem was proved from axioms:  ax-1 5  ax-2 6  ax-mp 7  ax-ia1 99  ax-ia2 100  ax-ia3 101  ax-in1 544  ax-in2 545  ax-io 630  ax-5 1336  ax-7 1337  ax-gen 1338  ax-ie1 1382  ax-ie2 1383  ax-8 1395  ax-10 1396  ax-11 1397  ax-i12 1398  ax-bndl 1399  ax-4 1400  ax-13 1404  ax-14 1405  ax-17 1419  ax-i9 1423  ax-ial 1427  ax-i5r 1428  ax-ext 2022  ax-coll 3872  ax-sep 3875  ax-nul 3883  ax-pow 3927  ax-pr 3944  ax-un 4170  ax-setind 4262  ax-iinf 4311

This theorem depends on definitions:  df-bi 110  df-dc 743  df-3or 886  df-3an 887  df-tru 1246  df-fal 1249  df-nf 1350  df-sb 1646  df-eu 1903  df-mo 1904  df-clab 2027  df-cleq 2033  df-clel 2036  df-nfc 2167  df-ne 2206  df-ral 2311  df-rex 2312  df-reu 2313  df-rab 2315  df-v 2559  df-sbc 2765  df-csb 2853  df-dif 2920  df-un 2922  df-in 2924  df-ss 2931  df-nul 3225  df-pw 3361  df-sn 3381  df-pr 3382  df-op 3384  df-uni 3581  df-int 3616  df-iun 3659  df-br 3765  df-opab 3819  df-mpt 3820  df-tr 3855  df-eprel 4026  df-id 4030  df-po 4033  df-iso 4034  df-iord 4103  df-on 4105  df-suc 4108  df-iom 4314  df-xp 4351  df-rel 4352  df-cnv 4353  df-co 4354  df-dm 4355  df-rn 4356  df-res 4357  df-ima 4358  df-iota 4867  df-fun 4904  df-fn 4905  df-f 4906  df-f1 4907  df-fo 4908  df-f1o 4909  df-fv 4910  df-ov 5515  df-oprab 5516  df-mpt2 5517  df-1st 5767  df-2nd 5768  df-recs 5920  df-irdg 5957  df-1o 6001  df-oadd 6005  df-omul 6006  df-er 6106  df-ec 6108  df-qs 6112  df-ni 6402  df-pli 6403  df-mi 6404  df-lti 6405  df-plpq 6442  df-mpq 6443  df-enq 6445  df-nqqs 6446  df-plqqs 6447  df-mqqs 6448  df-1nqqs 6449  df-rq 6450  df-ltnqqs 6451  df-inp 6564  df-iltp 6568

This theorem is referenced by:  caucvgprprlemrnd  6799