Theorem ltsopr 6694

Description: Positive real 'less than' is a weak linear order (in the sense of df-iso 4034). Proposition 11.2.3 of [HoTT], p. (varies). (Contributed by Jim Kingdon, 16-Dec-2019.)

Assertion

Ref	Expression
ltsopr	|- <P Or P.

Proof of Theorem ltsopr

Dummy variables r q s x y z are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		ltpopr 6693	. 2 |- <P Po P.
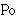2		ltdfpr 6604	. . . . 5 |- ( ( x e. P. /\ y e. P. ) -> ( x <P y <-> E. q e. Q. ( q e. ( 2nd ` x ) /\ q e. ( 1st ` y ) ) ) )
3	2	3adant3 924	. . . 4 |- ( ( x e. P. /\ y e. P. /\ z e. P. ) -> ( x <P y <-> E. q e. Q. ( q e. ( 2nd ` x ) /\ q e. ( 1st ` y ) ) ) )
4		prop 6573	. . . . . . . . . . . 12 |- ( x e. P. -> <. ( 1st ` x ) , ( 2nd ` x ) >. e. P. )
5		prnminu 6587	. . . . . . . . . . . 12 |- ( ( <. ( 1st ` x ) , ( 2nd ` x ) >. e. P. /\ q e. ( 2nd ` x ) ) -> E. r e. ( 2nd ` x ) r <Q q )
6	4, 5	sylan 267	. . . . . . . . . . 11 |- ( ( x e. P. /\ q e. ( 2nd ` x ) ) -> E. r e. ( 2nd ` x ) r <Q q )
7		prop 6573	. . . . . . . . . . . 12 |- ( y e. P. -> <. ( 1st ` y ) , ( 2nd ` y ) >. e. P. )
8		prnmaxl 6586	. . . . . . . . . . . 12 |- ( ( <. ( 1st ` y ) , ( 2nd ` y ) >. e. P. /\ q e. ( 1st ` y ) ) -> E. s e. ( 1st ` y ) q <Q s )
9	7, 8	sylan 267	. . . . . . . . . . 11 |- ( ( y e. P. /\ q e. ( 1st ` y ) ) -> E. s e. ( 1st ` y ) q <Q s )
10	6, 9	anim12i 321	. . . . . . . . . 10 |- ( ( ( x e. P. /\ q e. ( 2nd ` x ) ) /\ ( y e. P. /\ q e. ( 1st ` y ) ) ) -> ( E. r e. ( 2nd ` x ) r <Q q /\ E. s e. ( 1st ` y ) q <Q s ) )
11	10	an4s 522	. . . . . . . . 9 |- ( ( ( x e. P. /\ y e. P. ) /\ ( q e. ( 2nd ` x ) /\ q e. ( 1st ` y ) ) ) -> ( E. r e. ( 2nd ` x ) r <Q q /\ E. s e. ( 1st ` y ) q <Q s ) )
12		reeanv 2479	. . . . . . . . 9 |- ( E. r e. ( 2nd ` x ) E. s e. ( 1st ` y ) ( r <Q q /\ q <Q s ) <-> ( E. r e. ( 2nd ` x ) r <Q q /\ E. s e. ( 1st ` y ) q <Q s ) )
13	11, 12	sylibr 137	. . . . . . . 8 |- ( ( ( x e. P. /\ y e. P. ) /\ ( q e. ( 2nd ` x ) /\ q e. ( 1st ` y ) ) ) -> E. r e. ( 2nd ` x ) E. s e. ( 1st ` y ) ( r <Q q /\ q <Q s ) )
14	13	3adantl3 1062	. . . . . . 7 |- ( ( ( x e. P. /\ y e. P. /\ z e. P. ) /\ ( q e. ( 2nd ` x ) /\ q e. ( 1st ` y ) ) ) -> E. r e. ( 2nd ` x ) E. s e. ( 1st ` y ) ( r <Q q /\ q <Q s ) )
15		ltsonq 6496	. . . . . . . . . . . . 13 |- <Q Or Q.
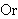16		ltrelnq 6463	. . . . . . . . . . . . 13 |- <Q C_ ( Q. X. Q. )
17	15, 16	sotri 4720	. . . . . . . . . . . 12 |- ( ( r <Q q /\ q <Q s ) -> r <Q s )
18	17	adantl 262	. . . . . . . . . . 11 |- ( ( ( ( ( x e. P. /\ y e. P. /\ z e. P. ) /\ ( q e. ( 2nd ` x ) /\ q e. ( 1st ` y ) ) ) /\ ( r e. ( 2nd ` x ) /\ s e. ( 1st ` y ) ) ) /\ ( r <Q q /\ q <Q s ) ) -> r <Q s )
19		prop 6573	. . . . . . . . . . . . . . . 16 |- ( z e. P. -> <. ( 1st ` z ) , ( 2nd ` z ) >. e. P. )
20		prloc 6589	. . . . . . . . . . . . . . . 16 |- ( ( <. ( 1st ` z ) , ( 2nd ` z ) >. e. P. /\ r <Q s ) -> ( r e. ( 1st ` z ) \/ s e. ( 2nd ` z ) ) )
21	19, 20	sylan 267	. . . . . . . . . . . . . . 15 |- ( ( z e. P. /\ r <Q s ) -> ( r e. ( 1st ` z ) \/ s e. ( 2nd ` z ) ) )
22	21	3ad2antl3 1068	. . . . . . . . . . . . . 14 |- ( ( ( x e. P. /\ y e. P. /\ z e. P. ) /\ r <Q s ) -> ( r e. ( 1st ` z ) \/ s e. ( 2nd ` z ) ) )
23	22	ex 108	. . . . . . . . . . . . 13 |- ( ( x e. P. /\ y e. P. /\ z e. P. ) -> ( r <Q s -> ( r e. ( 1st ` z ) \/ s e. ( 2nd ` z ) ) ) )
24	23	adantr 261	. . . . . . . . . . . 12 |- ( ( ( x e. P. /\ y e. P. /\ z e. P. ) /\ ( q e. ( 2nd ` x ) /\ q e. ( 1st ` y ) ) ) -> ( r <Q s -> ( r e. ( 1st ` z ) \/ s e. ( 2nd ` z ) ) ) )
25	24	ad2antrr 457	. . . . . . . . . . 11 |- ( ( ( ( ( x e. P. /\ y e. P. /\ z e. P. ) /\ ( q e. ( 2nd ` x ) /\ q e. ( 1st ` y ) ) ) /\ ( r e. ( 2nd ` x ) /\ s e. ( 1st ` y ) ) ) /\ ( r <Q q /\ q <Q s ) ) -> ( r <Q s -> ( r e. ( 1st ` z ) \/ s e. ( 2nd ` z ) ) ) )
26	18, 25	mpd 13	. . . . . . . . . 10 |- ( ( ( ( ( x e. P. /\ y e. P. /\ z e. P. ) /\ ( q e. ( 2nd ` x ) /\ q e. ( 1st ` y ) ) ) /\ ( r e. ( 2nd ` x ) /\ s e. ( 1st ` y ) ) ) /\ ( r <Q q /\ q <Q s ) ) -> ( r e. ( 1st ` z ) \/ s e. ( 2nd ` z ) ) )
27		elprnqu 6580	. . . . . . . . . . . . . . . . . . . . 21 |- ( ( <. ( 1st ` x ) , ( 2nd ` x ) >. e. P. /\ r e. ( 2nd ` x ) ) -> r e. Q. )
28	4, 27	sylan 267	. . . . . . . . . . . . . . . . . . . 20 |- ( ( x e. P. /\ r e. ( 2nd ` x ) ) -> r e. Q. )
29		ax-ia3 101	. . . . . . . . . . . . . . . . . . . . 21 |- ( r e. ( 2nd ` x ) -> ( r e. ( 1st ` z ) -> ( r e. ( 2nd ` x ) /\ r e. ( 1st ` z ) ) ) )
30	29	adantl 262	. . . . . . . . . . . . . . . . . . . 20 |- ( ( x e. P. /\ r e. ( 2nd ` x ) ) -> ( r e. ( 1st ` z ) -> ( r e. ( 2nd ` x ) /\ r e. ( 1st ` z ) ) ) )
31		19.8a 1482	. . . . . . . . . . . . . . . . . . . 20 |- ( ( r e. Q. /\ ( r e. ( 2nd ` x ) /\ r e. ( 1st ` z ) ) ) -> E. r ( r e. Q. /\ ( r e. ( 2nd ` x ) /\ r e. ( 1st ` z ) ) ) )
32	28, 30, 31	syl6an 1323	. . . . . . . . . . . . . . . . . . 19 |- ( ( x e. P. /\ r e. ( 2nd ` x ) ) -> ( r e. ( 1st ` z ) -> E. r ( r e. Q. /\ ( r e. ( 2nd ` x ) /\ r e. ( 1st ` z ) ) ) ) )
33	32	3ad2antl1 1066	. . . . . . . . . . . . . . . . . 18 |- ( ( ( x e. P. /\ y e. P. /\ z e. P. ) /\ r e. ( 2nd ` x ) ) -> ( r e. ( 1st ` z ) -> E. r ( r e. Q. /\ ( r e. ( 2nd ` x ) /\ r e. ( 1st ` z ) ) ) ) )
34	33	imp 115	. . . . . . . . . . . . . . . . 17 |- ( ( ( ( x e. P. /\ y e. P. /\ z e. P. ) /\ r e. ( 2nd ` x ) ) /\ r e. ( 1st ` z ) ) -> E. r ( r e. Q. /\ ( r e. ( 2nd ` x ) /\ r e. ( 1st ` z ) ) ) )
35		df-rex 2312	. . . . . . . . . . . . . . . . 17 |- ( E. r e. Q. ( r e. ( 2nd ` x ) /\ r e. ( 1st ` z ) ) <-> E. r ( r e. Q. /\ ( r e. ( 2nd ` x ) /\ r e. ( 1st ` z ) ) ) )
36	34, 35	sylibr 137	. . . . . . . . . . . . . . . 16 |- ( ( ( ( x e. P. /\ y e. P. /\ z e. P. ) /\ r e. ( 2nd ` x ) ) /\ r e. ( 1st ` z ) ) -> E. r e. Q. ( r e. ( 2nd ` x ) /\ r e. ( 1st ` z ) ) )
37		ltdfpr 6604	. . . . . . . . . . . . . . . . . . 19 |- ( ( x e. P. /\ z e. P. ) -> ( x <P z <-> E. r e. Q. ( r e. ( 2nd ` x ) /\ r e. ( 1st ` z ) ) ) )
38	37	biimprd 147	. . . . . . . . . . . . . . . . . 18 |- ( ( x e. P. /\ z e. P. ) -> ( E. r e. Q. ( r e. ( 2nd ` x ) /\ r e. ( 1st ` z ) ) -> x <P z ) )
39	38	3adant2 923	. . . . . . . . . . . . . . . . 17 |- ( ( x e. P. /\ y e. P. /\ z e. P. ) -> ( E. r e. Q. ( r e. ( 2nd ` x ) /\ r e. ( 1st ` z ) ) -> x <P z ) )
40	39	ad2antrr 457	. . . . . . . . . . . . . . . 16 |- ( ( ( ( x e. P. /\ y e. P. /\ z e. P. ) /\ r e. ( 2nd ` x ) ) /\ r e. ( 1st ` z ) ) -> ( E. r e. Q. ( r e. ( 2nd ` x ) /\ r e. ( 1st ` z ) ) -> x <P z ) )
41	36, 40	mpd 13	. . . . . . . . . . . . . . 15 |- ( ( ( ( x e. P. /\ y e. P. /\ z e. P. ) /\ r e. ( 2nd ` x ) ) /\ r e. ( 1st ` z ) ) -> x <P z )
42	41	ex 108	. . . . . . . . . . . . . 14 |- ( ( ( x e. P. /\ y e. P. /\ z e. P. ) /\ r e. ( 2nd ` x ) ) -> ( r e. ( 1st ` z ) -> x <P z ) )
43	42	adantrr 448	. . . . . . . . . . . . 13 |- ( ( ( x e. P. /\ y e. P. /\ z e. P. ) /\ ( r e. ( 2nd ` x ) /\ s e. ( 1st ` y ) ) ) -> ( r e. ( 1st ` z ) -> x <P z ) )
44		elprnql 6579	. . . . . . . . . . . . . . . . . . . . 21 |- ( ( <. ( 1st ` y ) , ( 2nd ` y ) >. e. P. /\ s e. ( 1st ` y ) ) -> s e. Q. )
45	7, 44	sylan 267	. . . . . . . . . . . . . . . . . . . 20 |- ( ( y e. P. /\ s e. ( 1st ` y ) ) -> s e. Q. )
46		pm3.21 251	. . . . . . . . . . . . . . . . . . . . 21 |- ( s e. ( 1st ` y ) -> ( s e. ( 2nd ` z ) -> ( s e. ( 2nd ` z ) /\ s e. ( 1st ` y ) ) ) )
47	46	adantl 262	. . . . . . . . . . . . . . . . . . . 20 |- ( ( y e. P. /\ s e. ( 1st ` y ) ) -> ( s e. ( 2nd ` z ) -> ( s e. ( 2nd ` z ) /\ s e. ( 1st ` y ) ) ) )
48		19.8a 1482	. . . . . . . . . . . . . . . . . . . 20 |- ( ( s e. Q. /\ ( s e. ( 2nd ` z ) /\ s e. ( 1st ` y ) ) ) -> E. s ( s e. Q. /\ ( s e. ( 2nd ` z ) /\ s e. ( 1st ` y ) ) ) )
49	45, 47, 48	syl6an 1323	. . . . . . . . . . . . . . . . . . 19 |- ( ( y e. P. /\ s e. ( 1st ` y ) ) -> ( s e. ( 2nd ` z ) -> E. s ( s e. Q. /\ ( s e. ( 2nd ` z ) /\ s e. ( 1st ` y ) ) ) ) )
50	49	3ad2antl2 1067	. . . . . . . . . . . . . . . . . 18 |- ( ( ( x e. P. /\ y e. P. /\ z e. P. ) /\ s e. ( 1st ` y ) ) -> ( s e. ( 2nd ` z ) -> E. s ( s e. Q. /\ ( s e. ( 2nd ` z ) /\ s e. ( 1st ` y ) ) ) ) )
51	50	imp 115	. . . . . . . . . . . . . . . . 17 |- ( ( ( ( x e. P. /\ y e. P. /\ z e. P. ) /\ s e. ( 1st ` y ) ) /\ s e. ( 2nd ` z ) ) -> E. s ( s e. Q. /\ ( s e. ( 2nd ` z ) /\ s e. ( 1st ` y ) ) ) )
52		df-rex 2312	. . . . . . . . . . . . . . . . 17 |- ( E. s e. Q. ( s e. ( 2nd ` z ) /\ s e. ( 1st ` y ) ) <-> E. s ( s e. Q. /\ ( s e. ( 2nd ` z ) /\ s e. ( 1st ` y ) ) ) )
53	51, 52	sylibr 137	. . . . . . . . . . . . . . . 16 |- ( ( ( ( x e. P. /\ y e. P. /\ z e. P. ) /\ s e. ( 1st ` y ) ) /\ s e. ( 2nd ` z ) ) -> E. s e. Q. ( s e. ( 2nd ` z ) /\ s e. ( 1st ` y ) ) )
54		ltdfpr 6604	. . . . . . . . . . . . . . . . . . . 20 |- ( ( z e. P. /\ y e. P. ) -> ( z <P y <-> E. s e. Q. ( s e. ( 2nd ` z ) /\ s e. ( 1st ` y ) ) ) )
55	54	biimprd 147	. . . . . . . . . . . . . . . . . . 19 |- ( ( z e. P. /\ y e. P. ) -> ( E. s e. Q. ( s e. ( 2nd ` z ) /\ s e. ( 1st ` y ) ) -> z <P y ) )
56	55	ancoms 255	. . . . . . . . . . . . . . . . . 18 |- ( ( y e. P. /\ z e. P. ) -> ( E. s e. Q. ( s e. ( 2nd ` z ) /\ s e. ( 1st ` y ) ) -> z <P y ) )
57	56	3adant1 922	. . . . . . . . . . . . . . . . 17 |- ( ( x e. P. /\ y e. P. /\ z e. P. ) -> ( E. s e. Q. ( s e. ( 2nd ` z ) /\ s e. ( 1st ` y ) ) -> z <P y ) )
58	57	ad2antrr 457	. . . . . . . . . . . . . . . 16 |- ( ( ( ( x e. P. /\ y e. P. /\ z e. P. ) /\ s e. ( 1st ` y ) ) /\ s e. ( 2nd ` z ) ) -> ( E. s e. Q. ( s e. ( 2nd ` z ) /\ s e. ( 1st ` y ) ) -> z <P y ) )
59	53, 58	mpd 13	. . . . . . . . . . . . . . 15 |- ( ( ( ( x e. P. /\ y e. P. /\ z e. P. ) /\ s e. ( 1st ` y ) ) /\ s e. ( 2nd ` z ) ) -> z <P y )
60	59	ex 108	. . . . . . . . . . . . . 14 |- ( ( ( x e. P. /\ y e. P. /\ z e. P. ) /\ s e. ( 1st ` y ) ) -> ( s e. ( 2nd ` z ) -> z <P y ) )
61	60	adantrl 447	. . . . . . . . . . . . 13 |- ( ( ( x e. P. /\ y e. P. /\ z e. P. ) /\ ( r e. ( 2nd ` x ) /\ s e. ( 1st ` y ) ) ) -> ( s e. ( 2nd ` z ) -> z <P y ) )
62	43, 61	orim12d 700	. . . . . . . . . . . 12 |- ( ( ( x e. P. /\ y e. P. /\ z e. P. ) /\ ( r e. ( 2nd ` x ) /\ s e. ( 1st ` y ) ) ) -> ( ( r e. ( 1st ` z ) \/ s e. ( 2nd ` z ) ) -> ( x <P z \/ z <P y ) ) )
63	62	adantlr 446	. . . . . . . . . . 11 |- ( ( ( ( x e. P. /\ y e. P. /\ z e. P. ) /\ ( q e. ( 2nd ` x ) /\ q e. ( 1st ` y ) ) ) /\ ( r e. ( 2nd ` x ) /\ s e. ( 1st ` y ) ) ) -> ( ( r e. ( 1st ` z ) \/ s e. ( 2nd ` z ) ) -> ( x <P z \/ z <P y ) ) )
64	63	adantr 261	. . . . . . . . . 10 |- ( ( ( ( ( x e. P. /\ y e. P. /\ z e. P. ) /\ ( q e. ( 2nd ` x ) /\ q e. ( 1st ` y ) ) ) /\ ( r e. ( 2nd ` x ) /\ s e. ( 1st ` y ) ) ) /\ ( r <Q q /\ q <Q s ) ) -> ( ( r e. ( 1st ` z ) \/ s e. ( 2nd ` z ) ) -> ( x <P z \/ z <P y ) ) )
65	26, 64	mpd 13	. . . . . . . . 9 |- ( ( ( ( ( x e. P. /\ y e. P. /\ z e. P. ) /\ ( q e. ( 2nd ` x ) /\ q e. ( 1st ` y ) ) ) /\ ( r e. ( 2nd ` x ) /\ s e. ( 1st ` y ) ) ) /\ ( r <Q q /\ q <Q s ) ) -> ( x <P z \/ z <P y ) )
66	65	ex 108	. . . . . . . 8 |- ( ( ( ( x e. P. /\ y e. P. /\ z e. P. ) /\ ( q e. ( 2nd ` x ) /\ q e. ( 1st ` y ) ) ) /\ ( r e. ( 2nd ` x ) /\ s e. ( 1st ` y ) ) ) -> ( ( r <Q q /\ q <Q s ) -> ( x <P z \/ z <P y ) ) )
67	66	rexlimdvva 2440	. . . . . . 7 |- ( ( ( x e. P. /\ y e. P. /\ z e. P. ) /\ ( q e. ( 2nd ` x ) /\ q e. ( 1st ` y ) ) ) -> ( E. r e. ( 2nd ` x ) E. s e. ( 1st ` y ) ( r <Q q /\ q <Q s ) -> ( x <P z \/ z <P y ) ) )
68	14, 67	mpd 13	. . . . . 6 |- ( ( ( x e. P. /\ y e. P. /\ z e. P. ) /\ ( q e. ( 2nd ` x ) /\ q e. ( 1st ` y ) ) ) -> ( x <P z \/ z <P y ) )
69	68	ex 108	. . . . 5 |- ( ( x e. P. /\ y e. P. /\ z e. P. ) -> ( ( q e. ( 2nd ` x ) /\ q e. ( 1st ` y ) ) -> ( x <P z \/ z <P y ) ) )
70	69	rexlimdvw 2436	. . . 4 |- ( ( x e. P. /\ y e. P. /\ z e. P. ) -> ( E. q e. Q. ( q e. ( 2nd ` x ) /\ q e. ( 1st ` y ) ) -> ( x <P z \/ z <P y ) ) )
71	3, 70	sylbid 139	. . 3 |- ( ( x e. P. /\ y e. P. /\ z e. P. ) -> ( x <P y -> ( x <P z \/ z <P y ) ) )
72	71	rgen3 2406	. 2 |- A. x e. P. A. y e. P. A. z e. P. ( x <P y -> ( x <P z \/ z <P y ) )
73		df-iso 4034	. 2 |- ( <P Or P. <-> ( <P Po P. /\ A. x e. P. A. y e. P. A. z e. P. ( x <P y -> ( x <P z \/ z <P y ) ) ) )
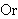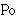
74	1, 72, 73	mpbir2an 849	1 |- <P Or P.

Syntax hints:   -> wi 4   /\ wa 97   <-> wb 98   \/ wo 629   /\ w3a 885   E.wex 1381   e. wcel 1393   A.wral 2306   E.wrex 2307   <.cop 3378   class class class wbr 3764   Po wpo 4031   Or wor 4032   ` cfv 4902   1stc1st 5765   2ndc2nd 5766   Q.cnq 6378   <Q cltq 6383   P.cnp 6389   <P cltp 6393

This theorem was proved from axioms:  ax-1 5  ax-2 6  ax-mp 7  ax-ia1 99  ax-ia2 100  ax-ia3 101  ax-in1 544  ax-in2 545  ax-io 630  ax-5 1336  ax-7 1337  ax-gen 1338  ax-ie1 1382  ax-ie2 1383  ax-8 1395  ax-10 1396  ax-11 1397  ax-i12 1398  ax-bndl 1399  ax-4 1400  ax-13 1404  ax-14 1405  ax-17 1419  ax-i9 1423  ax-ial 1427  ax-i5r 1428  ax-ext 2022  ax-coll 3872  ax-sep 3875  ax-nul 3883  ax-pow 3927  ax-pr 3944  ax-un 4170  ax-setind 4262  ax-iinf 4311

This theorem depends on definitions:  df-bi 110  df-dc 743  df-3or 886  df-3an 887  df-tru 1246  df-fal 1249  df-nf 1350  df-sb 1646  df-eu 1903  df-mo 1904  df-clab 2027  df-cleq 2033  df-clel 2036  df-nfc 2167  df-ne 2206  df-ral 2311  df-rex 2312  df-reu 2313  df-rab 2315  df-v 2559  df-sbc 2765  df-csb 2853  df-dif 2920  df-un 2922  df-in 2924  df-ss 2931  df-nul 3225  df-pw 3361  df-sn 3381  df-pr 3382  df-op 3384  df-uni 3581  df-int 3616  df-iun 3659  df-br 3765  df-opab 3819  df-mpt 3820  df-tr 3855  df-eprel 4026  df-id 4030  df-po 4033  df-iso 4034  df-iord 4103  df-on 4105  df-suc 4108  df-iom 4314  df-xp 4351  df-rel 4352  df-cnv 4353  df-co 4354  df-dm 4355  df-rn 4356  df-res 4357  df-ima 4358  df-iota 4867  df-fun 4904  df-fn 4905  df-f 4906  df-f1 4907  df-fo 4908  df-f1o 4909  df-fv 4910  df-ov 5515  df-oprab 5516  df-mpt2 5517  df-1st 5767  df-2nd 5768  df-recs 5920  df-irdg 5957  df-oadd 6005  df-omul 6006  df-er 6106  df-ec 6108  df-qs 6112  df-ni 6402  df-mi 6404  df-lti 6405  df-enq 6445  df-nqqs 6446  df-ltnqqs 6451  df-inp 6564  df-iltp 6568

This theorem is referenced by:  prplnqu  6718  addextpr  6719  caucvgprprlemk  6781  caucvgprprlemnkltj  6787  caucvgprprlemnkeqj  6788  caucvgprprlemnjltk  6789  caucvgprprlemnbj  6791  caucvgprprlemml  6792  caucvgprprlemlol  6796  caucvgprprlemupu  6798  caucvgprprlemloc  6801  caucvgprprlemaddq  6806  lttrsr  6847  ltposr  6848  ltsosr  6849  archsr  6866