ILE Home Intuitionistic Logic Explorer < Previous   Next >
Nearby theorems
Mirrors  >  Home  >  ILE Home  >  Th. List  >  indpi Unicode version
Theorem indpi 6440
Description: Principle of Finite Induction on positive integers. (Contributed by NM, 23-Mar-1996.)
Hypotheses
Ref Expression
indpi.1 |- ( x = 1o -> ( ph <-> ps ) )
indpi.2 |- ( x = y -> ( ph <-> ch ) )
indpi.3 |- ( x = ( y +N 1o ) -> ( ph <-> th ) )
indpi.4 |- ( x = A -> ( ph <-> ta ) )
indpi.5 |- ps
indpi.6 |- ( y e. N. -> ( ch -> th ) )
Assertion
Ref Expression
indpi |- ( A e. N. -> ta )
Distinct variable groups:   x, y   x, A   ps, x   ch, x   th, x   ta, x   ph, y
Allowed substitution hints:   ph( x)   ps( y)   ch( y)   th( y)   ta( y)   A( y)
Proof of Theorem indpi
StepHypRef Expression
1 indpi.4 . 2 |- ( x = A -> ( ph <-> ta ) )
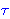2 elni 6406 . . 3 |- ( x e. N. <-> ( x e. om /\ x =/= (/) ) )
3 eqid 2040 . . . . . . . . . 10 |- (/) = (/)
43orci 650 . . . . . . . . 9 |- ( (/) = (/) \/ [. (/) / x ]. ph )
5 nfv 1421 . . . . . . . . . . 11 |- F/ x (/) = (/)
6 nfsbc1v 2782 . . . . . . . . . . 11 |- F/ x [. (/) / x ]. ph
75, 6nfor 1466 . . . . . . . . . 10 |- F/ x ( (/) = (/) \/ [. (/) / x ]. ph )
8 0ex 3884 . . . . . . . . . 10 |- (/) e. _V
9 eqeq1 2046 . . . . . . . . . . 11 |- ( x = (/) -> ( x = (/) <-> (/) = (/) ) )
10 sbceq1a 2773 . . . . . . . . . . 11 |- ( x = (/) -> ( ph <-> [. (/) / x ]. ph ) )
119, 10orbi12d 707 . . . . . . . . . 10 |- ( x = (/) -> ( ( x = (/) \/ ph ) <-> ( (/) = (/) \/ [. (/) / x ]. ph ) ) )
127, 8, 11elabf 2686 . . . . . . . . 9 |- ( (/) e. { x | ( x = (/) \/ ph ) } <-> ( (/) = (/) \/ [. (/) / x ]. ph ) )
134, 12mpbir 134 . . . . . . . 8 |- (/) e. { x | ( x = (/) \/ ph ) }
14 suceq 4139 . . . . . . . . . . . . . 14 |- ( y = (/) -> suc y = suc (/) )
15 df-1o 6001 . . . . . . . . . . . . . 14 |- 1o = suc (/)
1614, 15syl6eqr 2090 . . . . . . . . . . . . 13 |- ( y = (/) -> suc y = 1o )
17 indpi.5 . . . . . . . . . . . . . . 15 |- ps
1817olci 651 . . . . . . . . . . . . . 14 |- ( 1o = (/) \/ ps )
19 1onn 6093 . . . . . . . . . . . . . . . 16 |- 1o e. om
2019elexi 2567 . . . . . . . . . . . . . . 15 |- 1o e. _V
21 eqeq1 2046 . . . . . . . . . . . . . . . 16 |- ( x = 1o -> ( x = (/) <-> 1o = (/) ) )
22 indpi.1 . . . . . . . . . . . . . . . 16 |- ( x = 1o -> ( ph <-> ps ) )
2321, 22orbi12d 707 . . . . . . . . . . . . . . 15 |- ( x = 1o -> ( ( x = (/) \/ ph ) <-> ( 1o = (/) \/ ps ) ) )
2420, 23elab 2687 . . . . . . . . . . . . . 14 |- ( 1o e. { x | ( x = (/) \/ ph ) } <-> ( 1o = (/) \/ ps ) )
2518, 24mpbir 134 . . . . . . . . . . . . 13 |- 1o e. { x | ( x = (/) \/ ph ) }
2616, 25syl6eqel 2128 . . . . . . . . . . . 12 |- ( y = (/) -> suc y e. { x | ( x = (/) \/ ph ) } )
2726a1d 22 . . . . . . . . . . 11 |- ( y = (/) -> ( y e. { x | ( x = (/) \/ ph ) } -> suc y e. { x | ( x = (/) \/ ph ) } ) )
2827a1i 9 . . . . . . . . . 10 |- ( y e. om -> ( y = (/) -> ( y e. { x | ( x = (/) \/ ph ) } -> suc y e. { x | ( x = (/) \/ ph ) } ) ) )
29 indpi.6 . . . . . . . . . . . 12 |- ( y e. N. -> ( ch -> th ) )
30 elni 6406 . . . . . . . . . . . . . . . 16 |- ( y e. N. <-> ( y e. om /\ y =/= (/) ) )
3130simprbi 260 . . . . . . . . . . . . . . 15 |- ( y e. N. -> y =/= (/) )
3231neneqd 2226 . . . . . . . . . . . . . 14 |- ( y e. N. -> -. y = (/) )
33 biorf 663 . . . . . . . . . . . . . 14 |- ( -. y = (/) -> ( ch <-> ( y = (/) \/ ch ) ) )
3432, 33syl 14 . . . . . . . . . . . . 13 |- ( y e. N. -> ( ch <-> ( y = (/) \/ ch ) ) )
35 vex 2560 . . . . . . . . . . . . . 14 |- y e. _V
36 eqeq1 2046 . . . . . . . . . . . . . . 15 |- ( x = y -> ( x = (/) <-> y = (/) ) )
37 indpi.2 . . . . . . . . . . . . . . 15 |- ( x = y -> ( ph <-> ch ) )
3836, 37orbi12d 707 . . . . . . . . . . . . . 14 |- ( x = y -> ( ( x = (/) \/ ph ) <-> ( y = (/) \/ ch ) ) )
3935, 38elab 2687 . . . . . . . . . . . . 13 |- ( y e. { x | ( x = (/) \/ ph ) } <-> ( y = (/) \/ ch ) )
4034, 39syl6bbr 187 . . . . . . . . . . . 12 |- ( y e. N. -> ( ch <-> y e. { x | ( x = (/) \/ ph ) } ) )
41 1pi 6413 . . . . . . . . . . . . . . . . . 18 |- 1o e. N.
42 addclpi 6425 . . . . . . . . . . . . . . . . . 18 |- ( ( y e. N. /\ 1o e. N. ) -> ( y +N 1o ) e. N. )
4341, 42mpan2 401 . . . . . . . . . . . . . . . . 17 |- ( y e. N. -> ( y +N 1o ) e. N. )
44 elni 6406 . . . . . . . . . . . . . . . . 17 |- ( ( y +N 1o ) e. N. <-> ( ( y +N 1o ) e. om /\ ( y +N 1o ) =/= (/) ) )
4543, 44sylib 127 . . . . . . . . . . . . . . . 16 |- ( y e. N. -> ( ( y +N 1o ) e. om /\ ( y +N 1o ) =/= (/) ) )
4645simprd 107 . . . . . . . . . . . . . . 15 |- ( y e. N. -> ( y +N 1o ) =/= (/) )
4746neneqd 2226 . . . . . . . . . . . . . 14 |- ( y e. N. -> -. ( y +N 1o ) = (/) )
48 biorf 663 . . . . . . . . . . . . . 14 |- ( -. ( y +N 1o ) = (/) -> ( th <-> ( ( y +N 1o ) = (/) \/ th ) ) )
4947, 48syl 14 . . . . . . . . . . . . 13 |- ( y e. N. -> ( th <-> ( ( y +N 1o ) = (/) \/ th ) ) )
50 eqeq1 2046 . . . . . . . . . . . . . . . 16 |- ( x = ( y +N 1o ) -> ( x = (/) <-> ( y +N 1o ) = (/) ) )
51 indpi.3 . . . . . . . . . . . . . . . 16 |- ( x = ( y +N 1o ) -> ( ph <-> th ) )
5250, 51orbi12d 707 . . . . . . . . . . . . . . 15 |- ( x = ( y +N 1o ) -> ( ( x = (/) \/ ph ) <-> ( ( y +N 1o ) = (/) \/ th ) ) )
5352elabg 2688 . . . . . . . . . . . . . 14 |- ( ( y +N 1o ) e. N. -> ( ( y +N 1o ) e. { x | ( x = (/) \/ ph ) } <-> ( ( y +N 1o ) = (/) \/ th ) ) )
5443, 53syl 14 . . . . . . . . . . . . 13 |- ( y e. N. -> ( ( y +N 1o ) e. { x | ( x = (/) \/ ph ) } <-> ( ( y +N 1o ) = (/) \/ th ) ) )
55 addpiord 6414 . . . . . . . . . . . . . . . 16 |- ( ( y e. N. /\ 1o e. N. ) -> ( y +N 1o ) = ( y +o 1o ) )
5641, 55mpan2 401 . . . . . . . . . . . . . . 15 |- ( y e. N. -> ( y +N 1o ) = ( y +o 1o ) )
57 pion 6408 . . . . . . . . . . . . . . . 16 |- ( y e. N. -> y e. On )
58 oa1suc 6047 . . . . . . . . . . . . . . . 16 |- ( y e. On -> ( y +o 1o ) = suc y )
5957, 58syl 14 . . . . . . . . . . . . . . 15 |- ( y e. N. -> ( y +o 1o ) = suc y )
6056, 59eqtrd 2072 . . . . . . . . . . . . . 14 |- ( y e. N. -> ( y +N 1o ) = suc y )
6160eleq1d 2106 . . . . . . . . . . . . 13 |- ( y e. N. -> ( ( y +N 1o ) e. { x | ( x = (/) \/ ph ) } <-> suc y e. { x | ( x = (/) \/ ph ) } ) )
6249, 54, 613bitr2d 205 . . . . . . . . . . . 12 |- ( y e. N. -> ( th <-> suc y e. { x | ( x = (/) \/ ph ) } ) )
6329, 40, 623imtr3d 191 . . . . . . . . . . 11 |- ( y e. N. -> ( y e. { x | ( x = (/) \/ ph ) } -> suc y e. { x | ( x = (/) \/ ph ) } ) )
6463a1i 9 . . . . . . . . . 10 |- ( y e. om -> ( y e. N. -> ( y e. { x | ( x = (/) \/ ph ) } -> suc y e. { x | ( x = (/) \/ ph ) } ) ) )
65 nndceq0 4339 . . . . . . . . . . . 12 |- ( y e. om -> DECID y = (/) )
66 df-dc 743 . . . . . . . . . . . 12 |- (DECID y = (/) <-> ( y = (/) \/ -. y = (/) ) )
6765, 66sylib 127 . . . . . . . . . . 11 |- ( y e. om -> ( y = (/) \/ -. y = (/) ) )
68 idd 21 . . . . . . . . . . . . . . 15 |- ( y e. om -> ( y = (/) -> y = (/) ) )
6968necon3bd 2248 . . . . . . . . . . . . . 14 |- ( y e. om -> ( -. y = (/) -> y =/= (/) ) )
7069anc2li 312 . . . . . . . . . . . . 13 |- ( y e. om -> ( -. y = (/) -> ( y e. om /\ y =/= (/) ) ) )
7170, 30syl6ibr 151 . . . . . . . . . . . 12 |- ( y e. om -> ( -. y = (/) -> y e. N. ) )
7271orim2d 702 . . . . . . . . . . 11 |- ( y e. om -> ( ( y = (/) \/ -. y = (/) ) -> ( y = (/) \/ y e. N. ) ) )
7367, 72mpd 13 . . . . . . . . . 10 |- ( y e. om -> ( y = (/) \/ y e. N. ) )
7428, 64, 73mpjaod 638 . . . . . . . . 9 |- ( y e. om -> ( y e. { x | ( x = (/) \/ ph ) } -> suc y e. { x | ( x = (/) \/ ph ) } ) )
7574rgen 2374 . . . . . . . 8 |- A. y e. om ( y e. { x | ( x = (/) \/ ph ) } -> suc y e. { x | ( x = (/) \/ ph ) } )
76 peano5 4321 . . . . . . . 8 |- ( ( (/) e. { x | ( x = (/) \/ ph ) } /\ A. y e. om ( y e. { x | ( x = (/) \/ ph ) } -> suc y e. { x | ( x = (/) \/ ph ) } ) ) -> om C_ { x | ( x = (/) \/ ph ) } )
7713, 75, 76mp2an 402 . . . . . . 7 |- om C_ { x | ( x = (/) \/ ph ) }
7877sseli 2941 . . . . . 6 |- ( x e. om -> x e. { x | ( x = (/) \/ ph ) } )
79 abid 2028 . . . . . 6 |- ( x e. { x | ( x = (/) \/ ph ) } <-> ( x = (/) \/ ph ) )
8078, 79sylib 127 . . . . 5 |- ( x e. om -> ( x = (/) \/ ph ) )
8180adantr 261 . . . 4 |- ( ( x e. om /\ x =/= (/) ) -> ( x = (/) \/ ph ) )
82 df-ne 2206 . . . . . 6 |- ( x =/= (/) <-> -. x = (/) )
83 biorf 663 . . . . . 6 |- ( -. x = (/) -> ( ph <-> ( x = (/) \/ ph ) ) )
8482, 83sylbi 114 . . . . 5 |- ( x =/= (/) -> ( ph <-> ( x = (/) \/ ph ) ) )
8584adantl 262 . . . 4 |- ( ( x e. om /\ x =/= (/) ) -> ( ph <-> ( x = (/) \/ ph ) ) )
8681, 85mpbird 156 . . 3 |- ( ( x e. om /\ x =/= (/) ) -> ph )
872, 86sylbi 114 . 2 |- ( x e. N. -> ph )
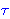881, 87vtoclga 2619 1 |- ( A e. N. -> ta )
Colors of variables: wff set class
Syntax hints:   -. wn 3   -> wi 4   /\ wa 97   <-> wb 98   \/ wo 629  DECID wdc 742   = wceq 1243   e. wcel 1393   {cab 2026   =/= wne 2204   A.wral 2306   [.wsbc 2764   C_ wss 2917   (/)c0 3224   Oncon0 4100   suc csuc 4102   omcom 4313  (class class class)co 5512   1oc1o 5994   +o coa 5998   N.cnpi 6370   +N cpli 6371
This theorem was proved from axioms:  ax-1 5  ax-2 6  ax-mp 7  ax-ia1 99  ax-ia2 100  ax-ia3 101  ax-in1 544  ax-in2 545  ax-io 630  ax-5 1336  ax-7 1337  ax-gen 1338  ax-ie1 1382  ax-ie2 1383  ax-8 1395  ax-10 1396  ax-11 1397  ax-i12 1398  ax-bndl 1399  ax-4 1400  ax-13 1404  ax-14 1405  ax-17 1419  ax-i9 1423  ax-ial 1427  ax-i5r 1428  ax-ext 2022  ax-coll 3872  ax-sep 3875  ax-nul 3883  ax-pow 3927  ax-pr 3944  ax-un 4170  ax-setind 4262  ax-iinf 4311
This theorem depends on definitions:  df-bi 110  df-dc 743  df-3an 887  df-tru 1246  df-fal 1249  df-nf 1350  df-sb 1646  df-eu 1903  df-mo 1904  df-clab 2027  df-cleq 2033  df-clel 2036  df-nfc 2167  df-ne 2206  df-ral 2311  df-rex 2312  df-reu 2313  df-rab 2315  df-v 2559  df-sbc 2765  df-csb 2853  df-dif 2920  df-un 2922  df-in 2924  df-ss 2931  df-nul 3225  df-pw 3361  df-sn 3381  df-pr 3382  df-op 3384  df-uni 3581  df-int 3616  df-iun 3659  df-br 3765  df-opab 3819  df-mpt 3820  df-tr 3855  df-id 4030  df-iord 4103  df-on 4105  df-suc 4108  df-iom 4314  df-xp 4351  df-rel 4352  df-cnv 4353  df-co 4354  df-dm 4355  df-rn 4356  df-res 4357  df-ima 4358  df-iota 4867  df-fun 4904  df-fn 4905  df-f 4906  df-f1 4907  df-fo 4908  df-f1o 4909  df-fv 4910  df-ov 5515  df-oprab 5516  df-mpt2 5517  df-1st 5767  df-2nd 5768  df-recs 5920  df-irdg 5957  df-1o 6001  df-oadd 6005  df-ni 6402  df-pli 6403
This theorem is referenced by:  pitonn  6924
  Copyright terms: Public domain W3C validator