Theorem eroveu 6197

Description: Lemma for eroprf 6199. (Contributed by Jeff Madsen, 10-Jun-2010.) (Revised by Mario Carneiro, 9-Jul-2014.)

Hypotheses

Ref	Expression
eropr.1	|- J = ( A /. R )
eropr.2	|- K = ( B /. S )
eropr.3	|- ( ph -> T e. Z )
eropr.4	|- ( ph -> R Er U )
eropr.5	|- ( ph -> S Er V )
eropr.6	|- ( ph -> T Er W )
eropr.7	|- ( ph -> A C_ U )
eropr.8	|- ( ph -> B C_ V )
eropr.9	|- ( ph -> C C_ W )
eropr.10	|- ( ph -> .+ : ( A X. B ) --> C )
eropr.11	|- ( ( ph /\ ( ( r e. A /\ s e. A ) /\ ( t e. B /\ u e. B ) ) ) -> ( ( r R s /\ t S u ) -> ( r .+ t ) T ( s .+ u ) ) )

Assertion

Ref	Expression
eroveu	|- ( ( ph /\ ( X e. J /\ Y e. K ) ) -> E! z E. p e. A E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ z = [ ( p .+ q ) ] T ) )

Distinct variable groups:   q, p, r, s, t, u, z, A   B, p, q, r, s, t, u, z   J, p, q, z   R, p, q, r, s, t, u, z   K, p, q, z   S, p, q, r, s, t, u, z   .+ , p, q, r, s, t, u, z   ph, p, q, r, s, t, u, z   T, p, q, r, s, t, u, z   X, p, q, r, s, t, u, z   Y, p, q, r, s, t, u, z

Allowed substitution hints:   C( z, u, t, s, r, q, p)   U( z, u, t, s, r, q, p)   J( u, t, s, r)   K( u, t, s, r)   V( z, u, t, s, r, q, p)   W( z, u, t, s, r, q, p)   Z( z, u, t, s, r, q, p)

Proof of Theorem eroveu

Dummy variable w is distinct from all other variables.

Step	Hyp	Ref	Expression
1		elqsi 6158	. . . . . . . 8 |- ( X e. ( A /. R ) -> E. p e. A X = [ p ] R )
2		eropr.1	. . . . . . . 8 |- J = ( A /. R )
3	1, 2	eleq2s 2132	. . . . . . 7 |- ( X e. J -> E. p e. A X = [ p ] R )
4		elqsi 6158	. . . . . . . 8 |- ( Y e. ( B /. S ) -> E. q e. B Y = [ q ] S )
5		eropr.2	. . . . . . . 8 |- K = ( B /. S )
6	4, 5	eleq2s 2132	. . . . . . 7 |- ( Y e. K -> E. q e. B Y = [ q ] S )
7	3, 6	anim12i 321	. . . . . 6 |- ( ( X e. J /\ Y e. K ) -> ( E. p e. A X = [ p ] R /\ E. q e. B Y = [ q ] S ) )
8	7	adantl 262	. . . . 5 |- ( ( ph /\ ( X e. J /\ Y e. K ) ) -> ( E. p e. A X = [ p ] R /\ E. q e. B Y = [ q ] S ) )
9		reeanv 2479	. . . . 5 |- ( E. p e. A E. q e. B ( X = [ p ] R /\ Y = [ q ] S ) <-> ( E. p e. A X = [ p ] R /\ E. q e. B Y = [ q ] S ) )
10	8, 9	sylibr 137	. . . 4 |- ( ( ph /\ ( X e. J /\ Y e. K ) ) -> E. p e. A E. q e. B ( X = [ p ] R /\ Y = [ q ] S ) )
11		eropr.3	. . . . . . . 8 |- ( ph -> T e. Z )
12	11	adantr 261	. . . . . . 7 |- ( ( ph /\ ( X e. J /\ Y e. K ) ) -> T e. Z )
13		ecexg 6110	. . . . . . 7 |- ( T e. Z -> [ ( p .+ q ) ] T e. _V )
14		elisset 2568	. . . . . . 7 |- ( [ ( p .+ q ) ] T e. _V -> E. z z = [ ( p .+ q ) ] T )
15	12, 13, 14	3syl 17	. . . . . 6 |- ( ( ph /\ ( X e. J /\ Y e. K ) ) -> E. z z = [ ( p .+ q ) ] T )
16	15	biantrud 288	. . . . 5 |- ( ( ph /\ ( X e. J /\ Y e. K ) ) -> ( ( X = [ p ] R /\ Y = [ q ] S ) <-> ( ( X = [ p ] R /\ Y = [ q ] S ) /\ E. z z = [ ( p .+ q ) ] T ) ) )
17	16	2rexbidv 2349	. . . 4 |- ( ( ph /\ ( X e. J /\ Y e. K ) ) -> ( E. p e. A E. q e. B ( X = [ p ] R /\ Y = [ q ] S ) <-> E. p e. A E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ E. z z = [ ( p .+ q ) ] T ) ) )
18	10, 17	mpbid 135	. . 3 |- ( ( ph /\ ( X e. J /\ Y e. K ) ) -> E. p e. A E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ E. z z = [ ( p .+ q ) ] T ) )
19		19.42v 1786	. . . . . . . 8 |- ( E. z ( ( X = [ p ] R /\ Y = [ q ] S ) /\ z = [ ( p .+ q ) ] T ) <-> ( ( X = [ p ] R /\ Y = [ q ] S ) /\ E. z z = [ ( p .+ q ) ] T ) )
20	19	bicomi 123	. . . . . . 7 |- ( ( ( X = [ p ] R /\ Y = [ q ] S ) /\ E. z z = [ ( p .+ q ) ] T ) <-> E. z ( ( X = [ p ] R /\ Y = [ q ] S ) /\ z = [ ( p .+ q ) ] T ) )
21	20	rexbii 2331	. . . . . 6 |- ( E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ E. z z = [ ( p .+ q ) ] T ) <-> E. q e. B E. z ( ( X = [ p ] R /\ Y = [ q ] S ) /\ z = [ ( p .+ q ) ] T ) )
22		rexcom4 2577	. . . . . 6 |- ( E. q e. B E. z ( ( X = [ p ] R /\ Y = [ q ] S ) /\ z = [ ( p .+ q ) ] T ) <-> E. z E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ z = [ ( p .+ q ) ] T ) )
23	21, 22	bitri 173	. . . . 5 |- ( E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ E. z z = [ ( p .+ q ) ] T ) <-> E. z E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ z = [ ( p .+ q ) ] T ) )
24	23	rexbii 2331	. . . 4 |- ( E. p e. A E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ E. z z = [ ( p .+ q ) ] T ) <-> E. p e. A E. z E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ z = [ ( p .+ q ) ] T ) )
25		rexcom4 2577	. . . 4 |- ( E. p e. A E. z E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ z = [ ( p .+ q ) ] T ) <-> E. z E. p e. A E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ z = [ ( p .+ q ) ] T ) )
26	24, 25	bitri 173	. . 3 |- ( E. p e. A E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ E. z z = [ ( p .+ q ) ] T ) <-> E. z E. p e. A E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ z = [ ( p .+ q ) ] T ) )
27	18, 26	sylib 127	. 2 |- ( ( ph /\ ( X e. J /\ Y e. K ) ) -> E. z E. p e. A E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ z = [ ( p .+ q ) ] T ) )
28		reeanv 2479	. . . . . 6 |- ( E. r e. A E. s e. A ( E. t e. B ( ( X = [ r ] R /\ Y = [ t ] S ) /\ z = [ ( r .+ t ) ] T ) /\ E. u e. B ( ( X = [ s ] R /\ Y = [ u ] S ) /\ w = [ ( s .+ u ) ] T ) ) <-> ( E. r e. A E. t e. B ( ( X = [ r ] R /\ Y = [ t ] S ) /\ z = [ ( r .+ t ) ] T ) /\ E. s e. A E. u e. B ( ( X = [ s ] R /\ Y = [ u ] S ) /\ w = [ ( s .+ u ) ] T ) ) )
29		eceq1 6141	. . . . . . . . . . 11 |- ( p = r -> [ p ] R = [ r ] R )
30	29	eqeq2d 2051	. . . . . . . . . 10 |- ( p = r -> ( X = [ p ] R <-> X = [ r ] R ) )
31	30	anbi1d 438	. . . . . . . . 9 |- ( p = r -> ( ( X = [ p ] R /\ Y = [ q ] S ) <-> ( X = [ r ] R /\ Y = [ q ] S ) ) )
32		oveq1 5519	. . . . . . . . . . 11 |- ( p = r -> ( p .+ q ) = ( r .+ q ) )
33	32	eceq1d 6142	. . . . . . . . . 10 |- ( p = r -> [ ( p .+ q ) ] T = [ ( r .+ q ) ] T )
34	33	eqeq2d 2051	. . . . . . . . 9 |- ( p = r -> ( z = [ ( p .+ q ) ] T <-> z = [ ( r .+ q ) ] T ) )
35	31, 34	anbi12d 442	. . . . . . . 8 |- ( p = r -> ( ( ( X = [ p ] R /\ Y = [ q ] S ) /\ z = [ ( p .+ q ) ] T ) <-> ( ( X = [ r ] R /\ Y = [ q ] S ) /\ z = [ ( r .+ q ) ] T ) ) )
36		eceq1 6141	. . . . . . . . . . 11 |- ( q = t -> [ q ] S = [ t ] S )
37	36	eqeq2d 2051	. . . . . . . . . 10 |- ( q = t -> ( Y = [ q ] S <-> Y = [ t ] S ) )
38	37	anbi2d 437	. . . . . . . . 9 |- ( q = t -> ( ( X = [ r ] R /\ Y = [ q ] S ) <-> ( X = [ r ] R /\ Y = [ t ] S ) ) )
39		oveq2 5520	. . . . . . . . . . 11 |- ( q = t -> ( r .+ q ) = ( r .+ t ) )
40	39	eceq1d 6142	. . . . . . . . . 10 |- ( q = t -> [ ( r .+ q ) ] T = [ ( r .+ t ) ] T )
41	40	eqeq2d 2051	. . . . . . . . 9 |- ( q = t -> ( z = [ ( r .+ q ) ] T <-> z = [ ( r .+ t ) ] T ) )
42	38, 41	anbi12d 442	. . . . . . . 8 |- ( q = t -> ( ( ( X = [ r ] R /\ Y = [ q ] S ) /\ z = [ ( r .+ q ) ] T ) <-> ( ( X = [ r ] R /\ Y = [ t ] S ) /\ z = [ ( r .+ t ) ] T ) ) )
43	35, 42	cbvrex2v 2542	. . . . . . 7 |- ( E. p e. A E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ z = [ ( p .+ q ) ] T ) <-> E. r e. A E. t e. B ( ( X = [ r ] R /\ Y = [ t ] S ) /\ z = [ ( r .+ t ) ] T ) )
44		eceq1 6141	. . . . . . . . . . 11 |- ( p = s -> [ p ] R = [ s ] R )
45	44	eqeq2d 2051	. . . . . . . . . 10 |- ( p = s -> ( X = [ p ] R <-> X = [ s ] R ) )
46	45	anbi1d 438	. . . . . . . . 9 |- ( p = s -> ( ( X = [ p ] R /\ Y = [ q ] S ) <-> ( X = [ s ] R /\ Y = [ q ] S ) ) )
47		oveq1 5519	. . . . . . . . . . 11 |- ( p = s -> ( p .+ q ) = ( s .+ q ) )
48	47	eceq1d 6142	. . . . . . . . . 10 |- ( p = s -> [ ( p .+ q ) ] T = [ ( s .+ q ) ] T )
49	48	eqeq2d 2051	. . . . . . . . 9 |- ( p = s -> ( w = [ ( p .+ q ) ] T <-> w = [ ( s .+ q ) ] T ) )
50	46, 49	anbi12d 442	. . . . . . . 8 |- ( p = s -> ( ( ( X = [ p ] R /\ Y = [ q ] S ) /\ w = [ ( p .+ q ) ] T ) <-> ( ( X = [ s ] R /\ Y = [ q ] S ) /\ w = [ ( s .+ q ) ] T ) ) )
51		eceq1 6141	. . . . . . . . . . 11 |- ( q = u -> [ q ] S = [ u ] S )
52	51	eqeq2d 2051	. . . . . . . . . 10 |- ( q = u -> ( Y = [ q ] S <-> Y = [ u ] S ) )
53	52	anbi2d 437	. . . . . . . . 9 |- ( q = u -> ( ( X = [ s ] R /\ Y = [ q ] S ) <-> ( X = [ s ] R /\ Y = [ u ] S ) ) )
54		oveq2 5520	. . . . . . . . . . 11 |- ( q = u -> ( s .+ q ) = ( s .+ u ) )
55	54	eceq1d 6142	. . . . . . . . . 10 |- ( q = u -> [ ( s .+ q ) ] T = [ ( s .+ u ) ] T )
56	55	eqeq2d 2051	. . . . . . . . 9 |- ( q = u -> ( w = [ ( s .+ q ) ] T <-> w = [ ( s .+ u ) ] T ) )
57	53, 56	anbi12d 442	. . . . . . . 8 |- ( q = u -> ( ( ( X = [ s ] R /\ Y = [ q ] S ) /\ w = [ ( s .+ q ) ] T ) <-> ( ( X = [ s ] R /\ Y = [ u ] S ) /\ w = [ ( s .+ u ) ] T ) ) )
58	50, 57	cbvrex2v 2542	. . . . . . 7 |- ( E. p e. A E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ w = [ ( p .+ q ) ] T ) <-> E. s e. A E. u e. B ( ( X = [ s ] R /\ Y = [ u ] S ) /\ w = [ ( s .+ u ) ] T ) )
59	43, 58	anbi12i 433	. . . . . 6 |- ( ( E. p e. A E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ z = [ ( p .+ q ) ] T ) /\ E. p e. A E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ w = [ ( p .+ q ) ] T ) ) <-> ( E. r e. A E. t e. B ( ( X = [ r ] R /\ Y = [ t ] S ) /\ z = [ ( r .+ t ) ] T ) /\ E. s e. A E. u e. B ( ( X = [ s ] R /\ Y = [ u ] S ) /\ w = [ ( s .+ u ) ] T ) ) )
60	28, 59	bitr4i 176	. . . . 5 |- ( E. r e. A E. s e. A ( E. t e. B ( ( X = [ r ] R /\ Y = [ t ] S ) /\ z = [ ( r .+ t ) ] T ) /\ E. u e. B ( ( X = [ s ] R /\ Y = [ u ] S ) /\ w = [ ( s .+ u ) ] T ) ) <-> ( E. p e. A E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ z = [ ( p .+ q ) ] T ) /\ E. p e. A E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ w = [ ( p .+ q ) ] T ) ) )
61		reeanv 2479	. . . . . . 7 |- ( E. t e. B E. u e. B ( ( ( X = [ r ] R /\ Y = [ t ] S ) /\ z = [ ( r .+ t ) ] T ) /\ ( ( X = [ s ] R /\ Y = [ u ] S ) /\ w = [ ( s .+ u ) ] T ) ) <-> ( E. t e. B ( ( X = [ r ] R /\ Y = [ t ] S ) /\ z = [ ( r .+ t ) ] T ) /\ E. u e. B ( ( X = [ s ] R /\ Y = [ u ] S ) /\ w = [ ( s .+ u ) ] T ) ) )
62		eropr.11	. . . . . . . . . . . . . 14 |- ( ( ph /\ ( ( r e. A /\ s e. A ) /\ ( t e. B /\ u e. B ) ) ) -> ( ( r R s /\ t S u ) -> ( r .+ t ) T ( s .+ u ) ) )
63		eropr.4	. . . . . . . . . . . . . . . . 17 |- ( ph -> R Er U )
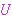64	63	adantr 261	. . . . . . . . . . . . . . . 16 |- ( ( ph /\ ( ( r e. A /\ s e. A ) /\ ( t e. B /\ u e. B ) ) ) -> R Er U )
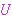65		eropr.7	. . . . . . . . . . . . . . . . . 18 |- ( ph -> A C_ U )
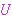66	65	adantr 261	. . . . . . . . . . . . . . . . 17 |- ( ( ph /\ ( ( r e. A /\ s e. A ) /\ ( t e. B /\ u e. B ) ) ) -> A C_ U )
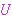67		simprll 489	. . . . . . . . . . . . . . . . 17 |- ( ( ph /\ ( ( r e. A /\ s e. A ) /\ ( t e. B /\ u e. B ) ) ) -> r e. A )
68	66, 67	sseldd 2946	. . . . . . . . . . . . . . . 16 |- ( ( ph /\ ( ( r e. A /\ s e. A ) /\ ( t e. B /\ u e. B ) ) ) -> r e. U )
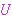69	64, 68	erth 6150	. . . . . . . . . . . . . . 15 |- ( ( ph /\ ( ( r e. A /\ s e. A ) /\ ( t e. B /\ u e. B ) ) ) -> ( r R s <-> [ r ] R = [ s ] R ) )
70		eropr.5	. . . . . . . . . . . . . . . . 17 |- ( ph -> S Er V )
71	70	adantr 261	. . . . . . . . . . . . . . . 16 |- ( ( ph /\ ( ( r e. A /\ s e. A ) /\ ( t e. B /\ u e. B ) ) ) -> S Er V )
72		eropr.8	. . . . . . . . . . . . . . . . . 18 |- ( ph -> B C_ V )
73	72	adantr 261	. . . . . . . . . . . . . . . . 17 |- ( ( ph /\ ( ( r e. A /\ s e. A ) /\ ( t e. B /\ u e. B ) ) ) -> B C_ V )
74		simprrl 491	. . . . . . . . . . . . . . . . 17 |- ( ( ph /\ ( ( r e. A /\ s e. A ) /\ ( t e. B /\ u e. B ) ) ) -> t e. B )
75	73, 74	sseldd 2946	. . . . . . . . . . . . . . . 16 |- ( ( ph /\ ( ( r e. A /\ s e. A ) /\ ( t e. B /\ u e. B ) ) ) -> t e. V )
76	71, 75	erth 6150	. . . . . . . . . . . . . . 15 |- ( ( ph /\ ( ( r e. A /\ s e. A ) /\ ( t e. B /\ u e. B ) ) ) -> ( t S u <-> [ t ] S = [ u ] S ) )
77	69, 76	anbi12d 442	. . . . . . . . . . . . . 14 |- ( ( ph /\ ( ( r e. A /\ s e. A ) /\ ( t e. B /\ u e. B ) ) ) -> ( ( r R s /\ t S u ) <-> ( [ r ] R = [ s ] R /\ [ t ] S = [ u ] S ) ) )
78		eropr.6	. . . . . . . . . . . . . . . 16 |- ( ph -> T Er W )
79	78	adantr 261	. . . . . . . . . . . . . . 15 |- ( ( ph /\ ( ( r e. A /\ s e. A ) /\ ( t e. B /\ u e. B ) ) ) -> T Er W )
80		eropr.9	. . . . . . . . . . . . . . . . 17 |- ( ph -> C C_ W )
81	80	adantr 261	. . . . . . . . . . . . . . . 16 |- ( ( ph /\ ( ( r e. A /\ s e. A ) /\ ( t e. B /\ u e. B ) ) ) -> C C_ W )
82		eropr.10	. . . . . . . . . . . . . . . . . 18 |- ( ph -> .+ : ( A X. B ) --> C )
83	82	adantr 261	. . . . . . . . . . . . . . . . 17 |- ( ( ph /\ ( ( r e. A /\ s e. A ) /\ ( t e. B /\ u e. B ) ) ) -> .+ : ( A X. B ) --> C )
84	83, 67, 74	fovrnd 5645	. . . . . . . . . . . . . . . 16 |- ( ( ph /\ ( ( r e. A /\ s e. A ) /\ ( t e. B /\ u e. B ) ) ) -> ( r .+ t ) e. C )
85	81, 84	sseldd 2946	. . . . . . . . . . . . . . 15 |- ( ( ph /\ ( ( r e. A /\ s e. A ) /\ ( t e. B /\ u e. B ) ) ) -> ( r .+ t ) e. W )
86	79, 85	erth 6150	. . . . . . . . . . . . . 14 |- ( ( ph /\ ( ( r e. A /\ s e. A ) /\ ( t e. B /\ u e. B ) ) ) -> ( ( r .+ t ) T ( s .+ u ) <-> [ ( r .+ t ) ] T = [ ( s .+ u ) ] T ) )
87	62, 77, 86	3imtr3d 191	. . . . . . . . . . . . 13 |- ( ( ph /\ ( ( r e. A /\ s e. A ) /\ ( t e. B /\ u e. B ) ) ) -> ( ( [ r ] R = [ s ] R /\ [ t ] S = [ u ] S ) -> [ ( r .+ t ) ] T = [ ( s .+ u ) ] T ) )
88		eqeq2 2049	. . . . . . . . . . . . . 14 |- ( w = [ ( s .+ u ) ] T -> ( [ ( r .+ t ) ] T = w <-> [ ( r .+ t ) ] T = [ ( s .+ u ) ] T ) )
89	88	biimprcd 149	. . . . . . . . . . . . 13 |- ( [ ( r .+ t ) ] T = [ ( s .+ u ) ] T -> ( w = [ ( s .+ u ) ] T -> [ ( r .+ t ) ] T = w ) )
90	87, 89	syl6 29	. . . . . . . . . . . 12 |- ( ( ph /\ ( ( r e. A /\ s e. A ) /\ ( t e. B /\ u e. B ) ) ) -> ( ( [ r ] R = [ s ] R /\ [ t ] S = [ u ] S ) -> ( w = [ ( s .+ u ) ] T -> [ ( r .+ t ) ] T = w ) ) )
91	90	impd 242	. . . . . . . . . . 11 |- ( ( ph /\ ( ( r e. A /\ s e. A ) /\ ( t e. B /\ u e. B ) ) ) -> ( ( ( [ r ] R = [ s ] R /\ [ t ] S = [ u ] S ) /\ w = [ ( s .+ u ) ] T ) -> [ ( r .+ t ) ] T = w ) )
92		eqeq1 2046	. . . . . . . . . . . . . . 15 |- ( X = [ r ] R -> ( X = [ s ] R <-> [ r ] R = [ s ] R ) )
93		eqeq1 2046	. . . . . . . . . . . . . . 15 |- ( Y = [ t ] S -> ( Y = [ u ] S <-> [ t ] S = [ u ] S ) )
94	92, 93	bi2anan9 538	. . . . . . . . . . . . . 14 |- ( ( X = [ r ] R /\ Y = [ t ] S ) -> ( ( X = [ s ] R /\ Y = [ u ] S ) <-> ( [ r ] R = [ s ] R /\ [ t ] S = [ u ] S ) ) )
95	94	anbi1d 438	. . . . . . . . . . . . 13 |- ( ( X = [ r ] R /\ Y = [ t ] S ) -> ( ( ( X = [ s ] R /\ Y = [ u ] S ) /\ w = [ ( s .+ u ) ] T ) <-> ( ( [ r ] R = [ s ] R /\ [ t ] S = [ u ] S ) /\ w = [ ( s .+ u ) ] T ) ) )
96	95	adantr 261	. . . . . . . . . . . 12 |- ( ( ( X = [ r ] R /\ Y = [ t ] S ) /\ z = [ ( r .+ t ) ] T ) -> ( ( ( X = [ s ] R /\ Y = [ u ] S ) /\ w = [ ( s .+ u ) ] T ) <-> ( ( [ r ] R = [ s ] R /\ [ t ] S = [ u ] S ) /\ w = [ ( s .+ u ) ] T ) ) )
97		eqeq1 2046	. . . . . . . . . . . . 13 |- ( z = [ ( r .+ t ) ] T -> ( z = w <-> [ ( r .+ t ) ] T = w ) )
98	97	adantl 262	. . . . . . . . . . . 12 |- ( ( ( X = [ r ] R /\ Y = [ t ] S ) /\ z = [ ( r .+ t ) ] T ) -> ( z = w <-> [ ( r .+ t ) ] T = w ) )
99	96, 98	imbi12d 223	. . . . . . . . . . 11 |- ( ( ( X = [ r ] R /\ Y = [ t ] S ) /\ z = [ ( r .+ t ) ] T ) -> ( ( ( ( X = [ s ] R /\ Y = [ u ] S ) /\ w = [ ( s .+ u ) ] T ) -> z = w ) <-> ( ( ( [ r ] R = [ s ] R /\ [ t ] S = [ u ] S ) /\ w = [ ( s .+ u ) ] T ) -> [ ( r .+ t ) ] T = w ) ) )
100	91, 99	syl5ibrcom 146	. . . . . . . . . 10 |- ( ( ph /\ ( ( r e. A /\ s e. A ) /\ ( t e. B /\ u e. B ) ) ) -> ( ( ( X = [ r ] R /\ Y = [ t ] S ) /\ z = [ ( r .+ t ) ] T ) -> ( ( ( X = [ s ] R /\ Y = [ u ] S ) /\ w = [ ( s .+ u ) ] T ) -> z = w ) ) )
101	100	impd 242	. . . . . . . . 9 |- ( ( ph /\ ( ( r e. A /\ s e. A ) /\ ( t e. B /\ u e. B ) ) ) -> ( ( ( ( X = [ r ] R /\ Y = [ t ] S ) /\ z = [ ( r .+ t ) ] T ) /\ ( ( X = [ s ] R /\ Y = [ u ] S ) /\ w = [ ( s .+ u ) ] T ) ) -> z = w ) )
102	101	anassrs 380	. . . . . . . 8 |- ( ( ( ph /\ ( r e. A /\ s e. A ) ) /\ ( t e. B /\ u e. B ) ) -> ( ( ( ( X = [ r ] R /\ Y = [ t ] S ) /\ z = [ ( r .+ t ) ] T ) /\ ( ( X = [ s ] R /\ Y = [ u ] S ) /\ w = [ ( s .+ u ) ] T ) ) -> z = w ) )
103	102	rexlimdvva 2440	. . . . . . 7 |- ( ( ph /\ ( r e. A /\ s e. A ) ) -> ( E. t e. B E. u e. B ( ( ( X = [ r ] R /\ Y = [ t ] S ) /\ z = [ ( r .+ t ) ] T ) /\ ( ( X = [ s ] R /\ Y = [ u ] S ) /\ w = [ ( s .+ u ) ] T ) ) -> z = w ) )
104	61, 103	syl5bir 142	. . . . . 6 |- ( ( ph /\ ( r e. A /\ s e. A ) ) -> ( ( E. t e. B ( ( X = [ r ] R /\ Y = [ t ] S ) /\ z = [ ( r .+ t ) ] T ) /\ E. u e. B ( ( X = [ s ] R /\ Y = [ u ] S ) /\ w = [ ( s .+ u ) ] T ) ) -> z = w ) )
105	104	rexlimdvva 2440	. . . . 5 |- ( ph -> ( E. r e. A E. s e. A ( E. t e. B ( ( X = [ r ] R /\ Y = [ t ] S ) /\ z = [ ( r .+ t ) ] T ) /\ E. u e. B ( ( X = [ s ] R /\ Y = [ u ] S ) /\ w = [ ( s .+ u ) ] T ) ) -> z = w ) )
106	60, 105	syl5bir 142	. . . 4 |- ( ph -> ( ( E. p e. A E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ z = [ ( p .+ q ) ] T ) /\ E. p e. A E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ w = [ ( p .+ q ) ] T ) ) -> z = w ) )
107	106	adantr 261	. . 3 |- ( ( ph /\ ( X e. J /\ Y e. K ) ) -> ( ( E. p e. A E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ z = [ ( p .+ q ) ] T ) /\ E. p e. A E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ w = [ ( p .+ q ) ] T ) ) -> z = w ) )
108	107	alrimivv 1755	. 2 |- ( ( ph /\ ( X e. J /\ Y e. K ) ) -> A. z A. w ( ( E. p e. A E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ z = [ ( p .+ q ) ] T ) /\ E. p e. A E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ w = [ ( p .+ q ) ] T ) ) -> z = w ) )
109		eqeq1 2046	. . . . 5 |- ( z = w -> ( z = [ ( p .+ q ) ] T <-> w = [ ( p .+ q ) ] T ) )
110	109	anbi2d 437	. . . 4 |- ( z = w -> ( ( ( X = [ p ] R /\ Y = [ q ] S ) /\ z = [ ( p .+ q ) ] T ) <-> ( ( X = [ p ] R /\ Y = [ q ] S ) /\ w = [ ( p .+ q ) ] T ) ) )
111	110	2rexbidv 2349	. . 3 |- ( z = w -> ( E. p e. A E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ z = [ ( p .+ q ) ] T ) <-> E. p e. A E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ w = [ ( p .+ q ) ] T ) ) )
112	111	eu4 1962	. 2 |- ( E! z E. p e. A E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ z = [ ( p .+ q ) ] T ) <-> ( E. z E. p e. A E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ z = [ ( p .+ q ) ] T ) /\ A. z A. w ( ( E. p e. A E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ z = [ ( p .+ q ) ] T ) /\ E. p e. A E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ w = [ ( p .+ q ) ] T ) ) -> z = w ) ) )
113	27, 108, 112	sylanbrc 394	1 |- ( ( ph /\ ( X e. J /\ Y e. K ) ) -> E! z E. p e. A E. q e. B ( ( X = [ p ] R /\ Y = [ q ] S ) /\ z = [ ( p .+ q ) ] T ) )

Syntax hints:   -> wi 4   /\ wa 97   <-> wb 98   A.wal 1241   = wceq 1243   E.wex 1381   e. wcel 1393   E!weu 1900   E.wrex 2307   _Vcvv 2557   C_ wss 2917   class class class wbr 3764   X. cxp 4343   -->wf 4898  (class class class)co 5512   Er wer 6103   [cec 6104   /.cqs 6105

This theorem was proved from axioms:  ax-1 5  ax-2 6  ax-mp 7  ax-ia1 99  ax-ia2 100  ax-ia3 101  ax-io 630  ax-5 1336  ax-7 1337  ax-gen 1338  ax-ie1 1382  ax-ie2 1383  ax-8 1395  ax-10 1396  ax-11 1397  ax-i12 1398  ax-bndl 1399  ax-4 1400  ax-13 1404  ax-14 1405  ax-17 1419  ax-i9 1423  ax-ial 1427  ax-i5r 1428  ax-ext 2022  ax-sep 3875  ax-pow 3927  ax-pr 3944  ax-un 4170

This theorem depends on definitions:  df-bi 110  df-3an 887  df-tru 1246  df-nf 1350  df-sb 1646  df-eu 1903  df-mo 1904  df-clab 2027  df-cleq 2033  df-clel 2036  df-nfc 2167  df-ral 2311  df-rex 2312  df-v 2559  df-sbc 2765  df-un 2922  df-in 2924  df-ss 2931  df-pw 3361  df-sn 3381  df-pr 3382  df-op 3384  df-uni 3581  df-br 3765  df-opab 3819  df-id 4030  df-xp 4351  df-rel 4352  df-cnv 4353  df-co 4354  df-dm 4355  df-rn 4356  df-res 4357  df-ima 4358  df-iota 4867  df-fun 4904  df-fn 4905  df-f 4906  df-fv 4910  df-ov 5515  df-er 6106  df-ec 6108  df-qs 6112

This theorem is referenced by:  erovlem  6198  eroprf  6199