Theorem euotd 3991

Description: Prove existential uniqueness for an ordered triple. (Contributed by Mario Carneiro, 20-May-2015.)

Hypotheses

Ref	Expression
euotd.1	|- ( ph -> A e. _V )
euotd.2	|- ( ph -> B e. _V )
euotd.3	|- ( ph -> C e. _V )
euotd.4	|- ( ph -> ( ps <-> ( a = A /\ b = B /\ c = C ) ) )

Assertion

Ref	Expression
euotd	|- ( ph -> E! x E. a E. b E. c ( x = <. a , b , c >. /\ ps ) )

Distinct variable groups:   a, b, c, x, A   B, a, b, c, x   C, a, b, c, x   ph, a, b, c, x

Allowed substitution hints:   ps( x, a, b, c)

Proof of Theorem euotd

Dummy variable y is distinct from all other variables.

Step	Hyp	Ref	Expression
1		euotd.1	. . . 4 |- ( ph -> A e. _V )
2		euotd.2	. . . 4 |- ( ph -> B e. _V )
3		euotd.3	. . . 4 |- ( ph -> C e. _V )
4		otexg 3967	. . . 4 |- ( ( A e. _V /\ B e. _V /\ C e. _V ) -> <. A , B , C >. e. _V )
5	1, 2, 3, 4	syl3anc 1135	. . 3 |- ( ph -> <. A , B , C >. e. _V )
6		euotd.4	. . . . . . . . . . . . 13 |- ( ph -> ( ps <-> ( a = A /\ b = B /\ c = C ) ) )
7	6	biimpa 280	. . . . . . . . . . . 12 |- ( ( ph /\ ps ) -> ( a = A /\ b = B /\ c = C ) )
8		vex 2560	. . . . . . . . . . . . 13 |- a e. _V
9		vex 2560	. . . . . . . . . . . . 13 |- b e. _V
10		vex 2560	. . . . . . . . . . . . 13 |- c e. _V
11	8, 9, 10	otth 3979	. . . . . . . . . . . 12 |- ( <. a , b , c >. = <. A , B , C >. <-> ( a = A /\ b = B /\ c = C ) )
12	7, 11	sylibr 137	. . . . . . . . . . 11 |- ( ( ph /\ ps ) -> <. a , b , c >. = <. A , B , C >. )
13	12	eqeq2d 2051	. . . . . . . . . 10 |- ( ( ph /\ ps ) -> ( x = <. a , b , c >. <-> x = <. A , B , C >. ) )
14	13	biimpd 132	. . . . . . . . 9 |- ( ( ph /\ ps ) -> ( x = <. a , b , c >. -> x = <. A , B , C >. ) )
15	14	impancom 247	. . . . . . . 8 |- ( ( ph /\ x = <. a , b , c >. ) -> ( ps -> x = <. A , B , C >. ) )
16	15	expimpd 345	. . . . . . 7 |- ( ph -> ( ( x = <. a , b , c >. /\ ps ) -> x = <. A , B , C >. ) )
17	16	exlimdv 1700	. . . . . 6 |- ( ph -> ( E. c ( x = <. a , b , c >. /\ ps ) -> x = <. A , B , C >. ) )
18	17	exlimdvv 1777	. . . . 5 |- ( ph -> ( E. a E. b E. c ( x = <. a , b , c >. /\ ps ) -> x = <. A , B , C >. ) )
19		tru 1247	. . . . . . . . . . 11 |- T.
20	2	adantr 261	. . . . . . . . . . . . 13 |- ( ( ph /\ a = A ) -> B e. _V )
21	3	ad2antrr 457	. . . . . . . . . . . . . 14 |- ( ( ( ph /\ a = A ) /\ b = B ) -> C e. _V )
22		simpr 103	. . . . . . . . . . . . . . . . . . 19 |- ( ( ph /\ ( a = A /\ b = B /\ c = C ) ) -> ( a = A /\ b = B /\ c = C ) )
23	22, 11	sylibr 137	. . . . . . . . . . . . . . . . . 18 |- ( ( ph /\ ( a = A /\ b = B /\ c = C ) ) -> <. a , b , c >. = <. A , B , C >. )
24	23	eqcomd 2045	. . . . . . . . . . . . . . . . 17 |- ( ( ph /\ ( a = A /\ b = B /\ c = C ) ) -> <. A , B , C >. = <. a , b , c >. )
25	6	biimpar 281	. . . . . . . . . . . . . . . . 17 |- ( ( ph /\ ( a = A /\ b = B /\ c = C ) ) -> ps )
26	24, 25	jca 290	. . . . . . . . . . . . . . . 16 |- ( ( ph /\ ( a = A /\ b = B /\ c = C ) ) -> ( <. A , B , C >. = <. a , b , c >. /\ ps ) )
27		a1tru 1259	. . . . . . . . . . . . . . . 16 |- ( ( ph /\ ( a = A /\ b = B /\ c = C ) ) -> T. )
28	26, 27	2thd 164	. . . . . . . . . . . . . . 15 |- ( ( ph /\ ( a = A /\ b = B /\ c = C ) ) -> ( ( <. A , B , C >. = <. a , b , c >. /\ ps ) <-> T. ) )
29	28	3anassrs 1126	. . . . . . . . . . . . . 14 |- ( ( ( ( ph /\ a = A ) /\ b = B ) /\ c = C ) -> ( ( <. A , B , C >. = <. a , b , c >. /\ ps ) <-> T. ) )
30	21, 29	sbcied 2799	. . . . . . . . . . . . 13 |- ( ( ( ph /\ a = A ) /\ b = B ) -> ( [. C / c ]. ( <. A , B , C >. = <. a , b , c >. /\ ps ) <-> T. ) )
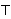31	20, 30	sbcied 2799	. . . . . . . . . . . 12 |- ( ( ph /\ a = A ) -> ( [. B / b ]. [. C / c ]. ( <. A , B , C >. = <. a , b , c >. /\ ps ) <-> T. ) )
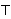32	1, 31	sbcied 2799	. . . . . . . . . . 11 |- ( ph -> ( [. A / a ]. [. B / b ]. [. C / c ]. ( <. A , B , C >. = <. a , b , c >. /\ ps ) <-> T. ) )
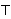33	19, 32	mpbiri 157	. . . . . . . . . 10 |- ( ph -> [. A / a ]. [. B / b ]. [. C / c ]. ( <. A , B , C >. = <. a , b , c >. /\ ps ) )
34	33	spesbcd 2844	. . . . . . . . 9 |- ( ph -> E. a [. B / b ]. [. C / c ]. ( <. A , B , C >. = <. a , b , c >. /\ ps ) )
35		nfcv 2178	. . . . . . . . . 10 |- F/_ b B
36		nfsbc1v 2782	. . . . . . . . . . 11 |- F/ b [. B / b ]. [. C / c ]. ( <. A , B , C >. = <. a , b , c >. /\ ps )
37	36	nfex 1528	. . . . . . . . . 10 |- F/ b E. a [. B / b ]. [. C / c ]. ( <. A , B , C >. = <. a , b , c >. /\ ps )
38		sbceq1a 2773	. . . . . . . . . . 11 |- ( b = B -> ( [. C / c ]. ( <. A , B , C >. = <. a , b , c >. /\ ps ) <-> [. B / b ]. [. C / c ]. ( <. A , B , C >. = <. a , b , c >. /\ ps ) ) )
39	38	exbidv 1706	. . . . . . . . . 10 |- ( b = B -> ( E. a [. C / c ]. ( <. A , B , C >. = <. a , b , c >. /\ ps ) <-> E. a [. B / b ]. [. C / c ]. ( <. A , B , C >. = <. a , b , c >. /\ ps ) ) )
40	35, 37, 39	spcegf 2636	. . . . . . . . 9 |- ( B e. _V -> ( E. a [. B / b ]. [. C / c ]. ( <. A , B , C >. = <. a , b , c >. /\ ps ) -> E. b E. a [. C / c ]. ( <. A , B , C >. = <. a , b , c >. /\ ps ) ) )
41	2, 34, 40	sylc 56	. . . . . . . 8 |- ( ph -> E. b E. a [. C / c ]. ( <. A , B , C >. = <. a , b , c >. /\ ps ) )
42		nfcv 2178	. . . . . . . . 9 |- F/_ c C
43		nfsbc1v 2782	. . . . . . . . . . 11 |- F/ c [. C / c ]. ( <. A , B , C >. = <. a , b , c >. /\ ps )
44	43	nfex 1528	. . . . . . . . . 10 |- F/ c E. a [. C / c ]. ( <. A , B , C >. = <. a , b , c >. /\ ps )
45	44	nfex 1528	. . . . . . . . 9 |- F/ c E. b E. a [. C / c ]. ( <. A , B , C >. = <. a , b , c >. /\ ps )
46		sbceq1a 2773	. . . . . . . . . 10 |- ( c = C -> ( ( <. A , B , C >. = <. a , b , c >. /\ ps ) <-> [. C / c ]. ( <. A , B , C >. = <. a , b , c >. /\ ps ) ) )
47	46	2exbidv 1748	. . . . . . . . 9 |- ( c = C -> ( E. b E. a ( <. A , B , C >. = <. a , b , c >. /\ ps ) <-> E. b E. a [. C / c ]. ( <. A , B , C >. = <. a , b , c >. /\ ps ) ) )
48	42, 45, 47	spcegf 2636	. . . . . . . 8 |- ( C e. _V -> ( E. b E. a [. C / c ]. ( <. A , B , C >. = <. a , b , c >. /\ ps ) -> E. c E. b E. a ( <. A , B , C >. = <. a , b , c >. /\ ps ) ) )
49	3, 41, 48	sylc 56	. . . . . . 7 |- ( ph -> E. c E. b E. a ( <. A , B , C >. = <. a , b , c >. /\ ps ) )
50		excom13 1579	. . . . . . 7 |- ( E. c E. b E. a ( <. A , B , C >. = <. a , b , c >. /\ ps ) <-> E. a E. b E. c ( <. A , B , C >. = <. a , b , c >. /\ ps ) )
51	49, 50	sylib 127	. . . . . 6 |- ( ph -> E. a E. b E. c ( <. A , B , C >. = <. a , b , c >. /\ ps ) )
52		eqeq1 2046	. . . . . . . 8 |- ( x = <. A , B , C >. -> ( x = <. a , b , c >. <-> <. A , B , C >. = <. a , b , c >. ) )
53	52	anbi1d 438	. . . . . . 7 |- ( x = <. A , B , C >. -> ( ( x = <. a , b , c >. /\ ps ) <-> ( <. A , B , C >. = <. a , b , c >. /\ ps ) ) )
54	53	3exbidv 1749	. . . . . 6 |- ( x = <. A , B , C >. -> ( E. a E. b E. c ( x = <. a , b , c >. /\ ps ) <-> E. a E. b E. c ( <. A , B , C >. = <. a , b , c >. /\ ps ) ) )
55	51, 54	syl5ibrcom 146	. . . . 5 |- ( ph -> ( x = <. A , B , C >. -> E. a E. b E. c ( x = <. a , b , c >. /\ ps ) ) )
56	18, 55	impbid 120	. . . 4 |- ( ph -> ( E. a E. b E. c ( x = <. a , b , c >. /\ ps ) <-> x = <. A , B , C >. ) )
57	56	alrimiv 1754	. . 3 |- ( ph -> A. x ( E. a E. b E. c ( x = <. a , b , c >. /\ ps ) <-> x = <. A , B , C >. ) )
58		eqeq2 2049	. . . . . 6 |- ( y = <. A , B , C >. -> ( x = y <-> x = <. A , B , C >. ) )
59	58	bibi2d 221	. . . . 5 |- ( y = <. A , B , C >. -> ( ( E. a E. b E. c ( x = <. a , b , c >. /\ ps ) <-> x = y ) <-> ( E. a E. b E. c ( x = <. a , b , c >. /\ ps ) <-> x = <. A , B , C >. ) ) )
60	59	albidv 1705	. . . 4 |- ( y = <. A , B , C >. -> ( A. x ( E. a E. b E. c ( x = <. a , b , c >. /\ ps ) <-> x = y ) <-> A. x ( E. a E. b E. c ( x = <. a , b , c >. /\ ps ) <-> x = <. A , B , C >. ) ) )
61	60	spcegv 2641	. . 3 |- ( <. A , B , C >. e. _V -> ( A. x ( E. a E. b E. c ( x = <. a , b , c >. /\ ps ) <-> x = <. A , B , C >. ) -> E. y A. x ( E. a E. b E. c ( x = <. a , b , c >. /\ ps ) <-> x = y ) ) )
62	5, 57, 61	sylc 56	. 2 |- ( ph -> E. y A. x ( E. a E. b E. c ( x = <. a , b , c >. /\ ps ) <-> x = y ) )
63		df-eu 1903	. 2 |- ( E! x E. a E. b E. c ( x = <. a , b , c >. /\ ps ) <-> E. y A. x ( E. a E. b E. c ( x = <. a , b , c >. /\ ps ) <-> x = y ) )
64	62, 63	sylibr 137	1 |- ( ph -> E! x E. a E. b E. c ( x = <. a , b , c >. /\ ps ) )

Syntax hints:   -> wi 4   /\ wa 97   <-> wb 98   /\ w3a 885   A.wal 1241   = wceq 1243   T. wtru 1244   E.wex 1381   e. wcel 1393   E!weu 1900   _Vcvv 2557   [.wsbc 2764   <.cotp 3379

This theorem was proved from axioms:  ax-1 5  ax-2 6  ax-mp 7  ax-ia1 99  ax-ia2 100  ax-ia3 101  ax-io 630  ax-5 1336  ax-7 1337  ax-gen 1338  ax-ie1 1382  ax-ie2 1383  ax-8 1395  ax-10 1396  ax-11 1397  ax-i12 1398  ax-bndl 1399  ax-4 1400  ax-14 1405  ax-17 1419  ax-i9 1423  ax-ial 1427  ax-i5r 1428  ax-ext 2022  ax-sep 3875  ax-pow 3927  ax-pr 3944

This theorem depends on definitions:  df-bi 110  df-3an 887  df-tru 1246  df-nf 1350  df-sb 1646  df-eu 1903  df-clab 2027  df-cleq 2033  df-clel 2036  df-nfc 2167  df-rex 2312  df-v 2559  df-sbc 2765  df-un 2922  df-in 2924  df-ss 2931  df-pw 3361  df-sn 3381  df-pr 3382  df-op 3384  df-ot 3385

This theorem is referenced by: (None)