Proof of Theorem xordidc
| Step | Hyp | Ref
| Expression |
|---|
| 1 | | dcbi 844 |
. . . . 5
  DECID DECID    DECID DECID   DECID DECID  
     |
| 2 | 1 | imp 115 |
. . . 4
   DECID DECID   DECID DECID  
 DECID
DECID   
   |
| 3 | | annimdc 845 |
. . . . . 6
  DECID DECID    DECID DECID         
        
      
      |
| 4 | 3 | imp 115 |
. . . . 5
   DECID DECID   DECID DECID               
    
     
     |
| 5 | | pm5.32 426 |
. . . . . 6
       
          
       |
| 6 | 5 | notbii 594 |
. . . . 5
            
   
      
    |
| 7 | 4, 6 | syl6bb 185 |
. . . 4
   DECID DECID   DECID DECID               
    
      
        |
| 8 | 2, 7 | sylan2 270 |
. . 3
   DECID DECID    DECID DECID   DECID
DECID            
    
      
        |
| 9 | | xornbidc 1282 |
. . . . . 6
  DECID DECID    DECID DECID      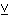    
        |
| 10 | 9 | imp 115 |
. . . . 5
   DECID DECID   DECID DECID  
    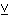
      
    |
| 11 | 10 | adantl 262 |
. . . 4
   DECID DECID    DECID DECID   DECID
DECID        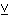    
       |
| 12 | 11 | anbi2d 437 |
. . 3
   DECID DECID    DECID DECID   DECID
DECID          
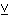           
     |
| 13 | | dcan 842 |
. . . . . 6
  DECID DECID    DECID DECID   DECID DECID        |
| 14 | 13 | imp 115 |
. . . . 5
   DECID DECID   DECID DECID    DECID DECID  
    |
| 15 | 14 | adantrr 448 |
. . . 4
   DECID DECID    DECID DECID   DECID
DECID     DECID DECID       |
| 16 | | dcan 842 |
. . . . . 6
  DECID DECID    DECID DECID   DECID DECID        |
| 17 | 16 | imp 115 |
. . . . 5
   DECID DECID   DECID DECID    DECID DECID  
    |
| 18 | 17 | adantrl 447 |
. . . 4
   DECID DECID    DECID DECID   DECID
DECID     DECID DECID       |
| 19 | | xornbidc 1282 |
. . . 4
  DECID DECID        DECID DECID              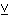              
          |
| 20 | 15, 18, 19 | sylc 56 |
. . 3
   DECID DECID    DECID DECID   DECID
DECID            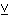              
         |
| 21 | 8, 12, 20 | 3bitr4d 209 |
. 2
   DECID DECID    DECID DECID   DECID
DECID          
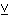           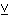         |
| 22 | 21 | exp32 347 |
1
  DECID DECID    DECID DECID    DECID DECID  
      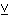    
      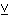           |