| Description: Axiom of Equality. One
of the equality and substitution axioms of
predicate calculus with equality. This is similar to, but not quite, a
transitive law for equality (proved later as equtr 1682). This axiom scheme
is a sub-scheme of Axiom Scheme B8 of system S2 of [Tarski], p. 75, whose
general form cannot be represented with our notation. Also appears as
Axiom C7 of [Monk2] p. 105 and Axiom Scheme
C8' in [Megill] p. 448 (p. 16
of the preprint).
The equality symbol was invented in 1527 by Robert Recorde. He chose a
pair of parallel lines of the same length because "noe .2. thynges,
can be
moare equalle."
Note that this axiom is still valid even when any two or all three of
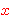 , ,  , and , and  are replaced with the same variable
since they
do not have any distinct variable (Metamath's $d) restrictions. Because
of this, we say that these three variables are "bundled" (a term
coined by
Raph Levien). (Contributed by NM, 5-Aug-1993.) are replaced with the same variable
since they
do not have any distinct variable (Metamath's $d) restrictions. Because
of this, we say that these three variables are "bundled" (a term
coined by
Raph Levien). (Contributed by NM, 5-Aug-1993.) |