Theorem funcnvuni 4968

Description: The union of a chain (with respect to inclusion) of single-rooted sets is single-rooted. (See funcnv 4960 for "single-rooted" definition.) (Contributed by NM, 11-Aug-2004.)

Assertion

Ref	Expression
funcnvuni	|- ( A. f e. A ( Fun `' f /\ A. g e. A ( f C_ g \/ g C_ f ) ) -> Fun `' U. A )

Distinct variable group:   f, g, A

Proof of Theorem funcnvuni

Dummy variables x y z w v are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		cnveq 4509	. . . . . . . 8 |- ( x = v -> `' x = `' v )
2	1	eqeq2d 2051	. . . . . . 7 |- ( x = v -> ( z = `' x <-> z = `' v ) )
3	2	cbvrexv 2534	. . . . . 6 |- ( E. x e. A z = `' x <-> E. v e. A z = `' v )
4		cnveq 4509	. . . . . . . . . . 11 |- ( f = v -> `' f = `' v )
5	4	funeqd 4923	. . . . . . . . . 10 |- ( f = v -> ( Fun `' f <-> Fun `' v ) )
6		sseq1 2966	. . . . . . . . . . . 12 |- ( f = v -> ( f C_ g <-> v C_ g ) )
7		sseq2 2967	. . . . . . . . . . . 12 |- ( f = v -> ( g C_ f <-> g C_ v ) )
8	6, 7	orbi12d 707	. . . . . . . . . . 11 |- ( f = v -> ( ( f C_ g \/ g C_ f ) <-> ( v C_ g \/ g C_ v ) ) )
9	8	ralbidv 2326	. . . . . . . . . 10 |- ( f = v -> ( A. g e. A ( f C_ g \/ g C_ f ) <-> A. g e. A ( v C_ g \/ g C_ v ) ) )
10	5, 9	anbi12d 442	. . . . . . . . 9 |- ( f = v -> ( ( Fun `' f /\ A. g e. A ( f C_ g \/ g C_ f ) ) <-> ( Fun `' v /\ A. g e. A ( v C_ g \/ g C_ v ) ) ) )
11	10	rspcv 2652	. . . . . . . 8 |- ( v e. A -> ( A. f e. A ( Fun `' f /\ A. g e. A ( f C_ g \/ g C_ f ) ) -> ( Fun `' v /\ A. g e. A ( v C_ g \/ g C_ v ) ) ) )
12		funeq 4921	. . . . . . . . . 10 |- ( z = `' v -> ( Fun z <-> Fun `' v ) )
13	12	biimprcd 149	. . . . . . . . 9 |- ( Fun `' v -> ( z = `' v -> Fun z ) )
14		sseq2 2967	. . . . . . . . . . . . . . 15 |- ( g = x -> ( v C_ g <-> v C_ x ) )
15		sseq1 2966	. . . . . . . . . . . . . . 15 |- ( g = x -> ( g C_ v <-> x C_ v ) )
16	14, 15	orbi12d 707	. . . . . . . . . . . . . 14 |- ( g = x -> ( ( v C_ g \/ g C_ v ) <-> ( v C_ x \/ x C_ v ) ) )
17	16	rspcv 2652	. . . . . . . . . . . . 13 |- ( x e. A -> ( A. g e. A ( v C_ g \/ g C_ v ) -> ( v C_ x \/ x C_ v ) ) )
18		cnvss 4508	. . . . . . . . . . . . . . . 16 |- ( v C_ x -> `' v C_ `' x )
19		cnvss 4508	. . . . . . . . . . . . . . . 16 |- ( x C_ v -> `' x C_ `' v )
20	18, 19	orim12i 676	. . . . . . . . . . . . . . 15 |- ( ( v C_ x \/ x C_ v ) -> ( `' v C_ `' x \/ `' x C_ `' v ) )
21		sseq12 2968	. . . . . . . . . . . . . . . . 17 |- ( ( z = `' v /\ w = `' x ) -> ( z C_ w <-> `' v C_ `' x ) )
22	21	ancoms 255	. . . . . . . . . . . . . . . 16 |- ( ( w = `' x /\ z = `' v ) -> ( z C_ w <-> `' v C_ `' x ) )
23		sseq12 2968	. . . . . . . . . . . . . . . 16 |- ( ( w = `' x /\ z = `' v ) -> ( w C_ z <-> `' x C_ `' v ) )
24	22, 23	orbi12d 707	. . . . . . . . . . . . . . 15 |- ( ( w = `' x /\ z = `' v ) -> ( ( z C_ w \/ w C_ z ) <-> ( `' v C_ `' x \/ `' x C_ `' v ) ) )
25	20, 24	syl5ibrcom 146	. . . . . . . . . . . . . 14 |- ( ( v C_ x \/ x C_ v ) -> ( ( w = `' x /\ z = `' v ) -> ( z C_ w \/ w C_ z ) ) )
26	25	expd 245	. . . . . . . . . . . . 13 |- ( ( v C_ x \/ x C_ v ) -> ( w = `' x -> ( z = `' v -> ( z C_ w \/ w C_ z ) ) ) )
27	17, 26	syl6com 31	. . . . . . . . . . . 12 |- ( A. g e. A ( v C_ g \/ g C_ v ) -> ( x e. A -> ( w = `' x -> ( z = `' v -> ( z C_ w \/ w C_ z ) ) ) ) )
28	27	rexlimdv 2432	. . . . . . . . . . 11 |- ( A. g e. A ( v C_ g \/ g C_ v ) -> ( E. x e. A w = `' x -> ( z = `' v -> ( z C_ w \/ w C_ z ) ) ) )
29	28	com23 72	. . . . . . . . . 10 |- ( A. g e. A ( v C_ g \/ g C_ v ) -> ( z = `' v -> ( E. x e. A w = `' x -> ( z C_ w \/ w C_ z ) ) ) )
30	29	alrimdv 1756	. . . . . . . . 9 |- ( A. g e. A ( v C_ g \/ g C_ v ) -> ( z = `' v -> A. w ( E. x e. A w = `' x -> ( z C_ w \/ w C_ z ) ) ) )
31	13, 30	anim12ii 325	. . . . . . . 8 |- ( ( Fun `' v /\ A. g e. A ( v C_ g \/ g C_ v ) ) -> ( z = `' v -> ( Fun z /\ A. w ( E. x e. A w = `' x -> ( z C_ w \/ w C_ z ) ) ) ) )
32	11, 31	syl6com 31	. . . . . . 7 |- ( A. f e. A ( Fun `' f /\ A. g e. A ( f C_ g \/ g C_ f ) ) -> ( v e. A -> ( z = `' v -> ( Fun z /\ A. w ( E. x e. A w = `' x -> ( z C_ w \/ w C_ z ) ) ) ) ) )
33	32	rexlimdv 2432	. . . . . 6 |- ( A. f e. A ( Fun `' f /\ A. g e. A ( f C_ g \/ g C_ f ) ) -> ( E. v e. A z = `' v -> ( Fun z /\ A. w ( E. x e. A w = `' x -> ( z C_ w \/ w C_ z ) ) ) ) )
34	3, 33	syl5bi 141	. . . . 5 |- ( A. f e. A ( Fun `' f /\ A. g e. A ( f C_ g \/ g C_ f ) ) -> ( E. x e. A z = `' x -> ( Fun z /\ A. w ( E. x e. A w = `' x -> ( z C_ w \/ w C_ z ) ) ) ) )
35	34	alrimiv 1754	. . . 4 |- ( A. f e. A ( Fun `' f /\ A. g e. A ( f C_ g \/ g C_ f ) ) -> A. z ( E. x e. A z = `' x -> ( Fun z /\ A. w ( E. x e. A w = `' x -> ( z C_ w \/ w C_ z ) ) ) ) )
36		df-ral 2311	. . . . 5 |- ( A. z e. { y | E. x e. A y = `' x } ( Fun z /\ A. w e. { y | E. x e. A y = `' x } ( z C_ w \/ w C_ z ) ) <-> A. z ( z e. { y | E. x e. A y = `' x } -> ( Fun z /\ A. w e. { y | E. x e. A y = `' x } ( z C_ w \/ w C_ z ) ) ) )
37		vex 2560	. . . . . . . 8 |- z e. _V
38		eqeq1 2046	. . . . . . . . 9 |- ( y = z -> ( y = `' x <-> z = `' x ) )
39	38	rexbidv 2327	. . . . . . . 8 |- ( y = z -> ( E. x e. A y = `' x <-> E. x e. A z = `' x ) )
40	37, 39	elab 2687	. . . . . . 7 |- ( z e. { y | E. x e. A y = `' x } <-> E. x e. A z = `' x )
41		eqeq1 2046	. . . . . . . . . 10 |- ( y = w -> ( y = `' x <-> w = `' x ) )
42	41	rexbidv 2327	. . . . . . . . 9 |- ( y = w -> ( E. x e. A y = `' x <-> E. x e. A w = `' x ) )
43	42	ralab 2701	. . . . . . . 8 |- ( A. w e. { y | E. x e. A y = `' x } ( z C_ w \/ w C_ z ) <-> A. w ( E. x e. A w = `' x -> ( z C_ w \/ w C_ z ) ) )
44	43	anbi2i 430	. . . . . . 7 |- ( ( Fun z /\ A. w e. { y | E. x e. A y = `' x } ( z C_ w \/ w C_ z ) ) <-> ( Fun z /\ A. w ( E. x e. A w = `' x -> ( z C_ w \/ w C_ z ) ) ) )
45	40, 44	imbi12i 228	. . . . . 6 |- ( ( z e. { y | E. x e. A y = `' x } -> ( Fun z /\ A. w e. { y | E. x e. A y = `' x } ( z C_ w \/ w C_ z ) ) ) <-> ( E. x e. A z = `' x -> ( Fun z /\ A. w ( E. x e. A w = `' x -> ( z C_ w \/ w C_ z ) ) ) ) )
46	45	albii 1359	. . . . 5 |- ( A. z ( z e. { y | E. x e. A y = `' x } -> ( Fun z /\ A. w e. { y | E. x e. A y = `' x } ( z C_ w \/ w C_ z ) ) ) <-> A. z ( E. x e. A z = `' x -> ( Fun z /\ A. w ( E. x e. A w = `' x -> ( z C_ w \/ w C_ z ) ) ) ) )
47	36, 46	bitr2i 174	. . . 4 |- ( A. z ( E. x e. A z = `' x -> ( Fun z /\ A. w ( E. x e. A w = `' x -> ( z C_ w \/ w C_ z ) ) ) ) <-> A. z e. { y | E. x e. A y = `' x } ( Fun z /\ A. w e. { y | E. x e. A y = `' x } ( z C_ w \/ w C_ z ) ) )
48	35, 47	sylib 127	. . 3 |- ( A. f e. A ( Fun `' f /\ A. g e. A ( f C_ g \/ g C_ f ) ) -> A. z e. { y | E. x e. A y = `' x } ( Fun z /\ A. w e. { y | E. x e. A y = `' x } ( z C_ w \/ w C_ z ) ) )
49		fununi 4967	. . 3 |- ( A. z e. { y | E. x e. A y = `' x } ( Fun z /\ A. w e. { y | E. x e. A y = `' x } ( z C_ w \/ w C_ z ) ) -> Fun U. { y | E. x e. A y = `' x } )
50	48, 49	syl 14	. 2 |- ( A. f e. A ( Fun `' f /\ A. g e. A ( f C_ g \/ g C_ f ) ) -> Fun U. { y | E. x e. A y = `' x } )
51		cnvuni 4521	. . . 4 |- `' U. A = U_ x e. A `' x
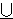52		vex 2560	. . . . . 6 |- x e. _V
53	52	cnvex 4856	. . . . 5 |- `' x e. _V
54	53	dfiun2 3691	. . . 4 |- U_ x e. A `' x = U. { y | E. x e. A y = `' x }
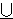
55	51, 54	eqtri 2060	. . 3 |- `' U. A = U. { y | E. x e. A y = `' x }
56	55	funeqi 4922	. 2 |- ( Fun `' U. A <-> Fun U. { y | E. x e. A y = `' x } )
57	50, 56	sylibr 137	1 |- ( A. f e. A ( Fun `' f /\ A. g e. A ( f C_ g \/ g C_ f ) ) -> Fun `' U. A )

Syntax hints:   -> wi 4   /\ wa 97   <-> wb 98   \/ wo 629   A.wal 1241   = wceq 1243   e. wcel 1393   {cab 2026   A.wral 2306   E.wrex 2307   C_ wss 2917   U.cuni 3580   U_ciun 3657   `'ccnv 4344   Fun wfun 4896

This theorem was proved from axioms:  ax-1 5  ax-2 6  ax-mp 7  ax-ia1 99  ax-ia2 100  ax-ia3 101  ax-io 630  ax-5 1336  ax-7 1337  ax-gen 1338  ax-ie1 1382  ax-ie2 1383  ax-8 1395  ax-10 1396  ax-11 1397  ax-i12 1398  ax-bndl 1399  ax-4 1400  ax-13 1404  ax-14 1405  ax-17 1419  ax-i9 1423  ax-ial 1427  ax-i5r 1428  ax-ext 2022  ax-sep 3875  ax-pow 3927  ax-pr 3944  ax-un 4170

This theorem depends on definitions:  df-bi 110  df-3an 887  df-tru 1246  df-nf 1350  df-sb 1646  df-eu 1903  df-mo 1904  df-clab 2027  df-cleq 2033  df-clel 2036  df-nfc 2167  df-ral 2311  df-rex 2312  df-v 2559  df-un 2922  df-in 2924  df-ss 2931  df-pw 3361  df-sn 3381  df-pr 3382  df-op 3384  df-uni 3581  df-iun 3659  df-br 3765  df-opab 3819  df-id 4030  df-xp 4351  df-rel 4352  df-cnv 4353  df-co 4354  df-dm 4355  df-rn 4356  df-fun 4904

This theorem is referenced by:  fun11uni  4969