Description: Define the limit ordinal
predicate, which is true for an ordinal that has
the empty set as an element and is not a successor (i.e. that is the union
of itself). Our definition combines the definition of Lim of
[BellMachover] p. 471 and Exercise 1
of [TakeutiZaring] p. 42, and then
changes  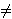 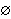 to to 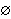 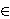  (which would be equivalent given the
law of the excluded middle, but which is not for us). (Contributed by Jim
Kingdon, 11-Nov-2018.) Use its alias dflim2 4107 instead for naming
consistency with set.mm. (New usage is
discouraged.) (which would be equivalent given the
law of the excluded middle, but which is not for us). (Contributed by Jim
Kingdon, 11-Nov-2018.) Use its alias dflim2 4107 instead for naming
consistency with set.mm. (New usage is
discouraged.) |