Description: This syntax construction
states that a variable  , which has been
declared to be a setvar variable by $f statement vx, is also a class
expression. This can be justified informally as follows. We know that
the class builder , which has been
declared to be a setvar variable by $f statement vx, is also a class
expression. This can be justified informally as follows. We know that
the class builder 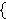  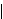  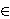  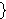 is a class by cab 2026.
Since (when is a class by cab 2026.
Since (when
 is distinct from is distinct from
 ) we have ) we have  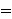 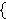  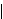  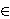  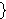 by
cvjust 2035, we can argue that the syntax " by
cvjust 2035, we can argue that the syntax "  " can be viewed as
an abbreviation for " " can be viewed as
an abbreviation for " 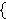    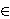  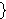 ". See the
discussion
under the definition of class in [Jech] p.
4 showing that "Every set can
be considered to be a class." ". See the
discussion
under the definition of class in [Jech] p.
4 showing that "Every set can
be considered to be a class."
While it is tempting and perhaps occasionally useful to view cv 1242 as a
"type conversion" from a setvar variable to a class variable,
keep in
mind that cv 1242 is intrinsically no different from any other
class-building syntax such as cab 2026, cun 2915,
or c0 3224.
For a general discussion of the theory of classes and the role of cv 1242,
see http://us.metamath.org/mpeuni/mmset.html#class.
(The description above applies to set theory, not predicate calculus.
The purpose of introducing   here, and not in set theory where
it belongs, is to allow us to express i.e. "prove" the weq 1392 of
predicate calculus from the wceq 1243 of set theory, so that we don't
overload the here, and not in set theory where
it belongs, is to allow us to express i.e. "prove" the weq 1392 of
predicate calculus from the wceq 1243 of set theory, so that we don't
overload the 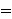 connective with two syntax definitions. This is done
to prevent ambiguity that would complicate some Metamath
parsers.)
connective with two syntax definitions. This is done
to prevent ambiguity that would complicate some Metamath
parsers.) |