Description: "Barbara", one
of the fundamental syllogisms of Aristotelian logic. All
 is is  , and all , and all  is is  , therefore all , therefore all  is is
 . (In
Aristotelian notation, AAA-1: MaP and SaM therefore SaP.)
For example, given "All men are mortal" and "Socrates is
a man", we can
prove "Socrates is mortal". If H is the set of men, M is the
set of
mortal beings, and S is Socrates, these word phrases can be represented
as . (In
Aristotelian notation, AAA-1: MaP and SaM therefore SaP.)
For example, given "All men are mortal" and "Socrates is
a man", we can
prove "Socrates is mortal". If H is the set of men, M is the
set of
mortal beings, and S is Socrates, these word phrases can be represented
as 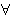 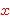 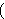 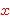 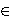  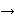 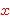 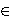
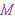 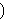 (all men are mortal) and (all men are mortal) and
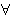 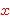 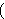 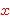 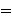 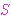 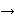 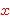 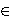
  (Socrates is a man) therefore (Socrates is a man) therefore
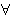 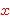 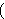 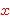 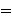 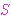 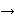 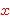 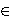
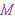 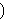 (Socrates is mortal). Russell and
Whitehead note that the "syllogism in Barbara is derived..."
from
syl 14. (quote after Theorem *2.06 of [WhiteheadRussell] p. 101). Most
of the proof is in alsyl 1526. There are a legion of sources for Barbara,
including http://www.friesian.com/aristotl.htm,
http://plato.stanford.edu/entries/aristotle-logic/,
and
https://en.wikipedia.org/wiki/Syllogism.
(Contributed by David A.
Wheeler, 24-Aug-2016.) (Socrates is mortal). Russell and
Whitehead note that the "syllogism in Barbara is derived..."
from
syl 14. (quote after Theorem *2.06 of [WhiteheadRussell] p. 101). Most
of the proof is in alsyl 1526. There are a legion of sources for Barbara,
including http://www.friesian.com/aristotl.htm,
http://plato.stanford.edu/entries/aristotle-logic/,
and
https://en.wikipedia.org/wiki/Syllogism.
(Contributed by David A.
Wheeler, 24-Aug-2016.) |