Theorem ac6sfi 6352

Description: Existence of a choice function for finite sets. (Contributed by Jeff Hankins, 26-Jun-2009.) (Proof shortened by Mario Carneiro, 29-Jan-2014.)

Hypothesis

Ref	Expression
ac6sfi.1	|- ( y = ( f ` x ) -> ( ph <-> ps ) )

Assertion

Ref	Expression
ac6sfi	|- ( ( A e. Fin /\ A. x e. A E. y e. B ph ) -> E. f ( f : A --> B /\ A. x e. A ps ) )

Distinct variable groups:   x, f, A   y, f, B, x   ph, f   ps, y

Allowed substitution hints:   ph( x, y)   ps( x, f)   A( y)

Proof of Theorem ac6sfi

Dummy variables u w z g are mutually distinct and distinct from all other variables.

Step	Hyp	Ref	Expression
1		raleq 2505	. . . 4 |- ( u = (/) -> ( A. x e. u E. y e. B ph <-> A. x e. (/) E. y e. B ph ) )
2		feq2 5031	. . . . . 6 |- ( u = (/) -> ( f : u --> B <-> f : (/) --> B ) )
3		raleq 2505	. . . . . 6 |- ( u = (/) -> ( A. x e. u ps <-> A. x e. (/) ps ) )
4	2, 3	anbi12d 442	. . . . 5 |- ( u = (/) -> ( ( f : u --> B /\ A. x e. u ps ) <-> ( f : (/) --> B /\ A. x e. (/) ps ) ) )
5	4	exbidv 1706	. . . 4 |- ( u = (/) -> ( E. f ( f : u --> B /\ A. x e. u ps ) <-> E. f ( f : (/) --> B /\ A. x e. (/) ps ) ) )
6	1, 5	imbi12d 223	. . 3 |- ( u = (/) -> ( ( A. x e. u E. y e. B ph -> E. f ( f : u --> B /\ A. x e. u ps ) ) <-> ( A. x e. (/) E. y e. B ph -> E. f ( f : (/) --> B /\ A. x e. (/) ps ) ) ) )
7		raleq 2505	. . . 4 |- ( u = w -> ( A. x e. u E. y e. B ph <-> A. x e. w E. y e. B ph ) )
8		feq2 5031	. . . . . 6 |- ( u = w -> ( f : u --> B <-> f : w --> B ) )
9		raleq 2505	. . . . . 6 |- ( u = w -> ( A. x e. u ps <-> A. x e. w ps ) )
10	8, 9	anbi12d 442	. . . . 5 |- ( u = w -> ( ( f : u --> B /\ A. x e. u ps ) <-> ( f : w --> B /\ A. x e. w ps ) ) )
11	10	exbidv 1706	. . . 4 |- ( u = w -> ( E. f ( f : u --> B /\ A. x e. u ps ) <-> E. f ( f : w --> B /\ A. x e. w ps ) ) )
12	7, 11	imbi12d 223	. . 3 |- ( u = w -> ( ( A. x e. u E. y e. B ph -> E. f ( f : u --> B /\ A. x e. u ps ) ) <-> ( A. x e. w E. y e. B ph -> E. f ( f : w --> B /\ A. x e. w ps ) ) ) )
13		raleq 2505	. . . 4 |- ( u = ( w u. { z } ) -> ( A. x e. u E. y e. B ph <-> A. x e. ( w u. { z } ) E. y e. B ph ) )
14		feq2 5031	. . . . . . 7 |- ( u = ( w u. { z } ) -> ( f : u --> B <-> f : ( w u. { z } ) --> B ) )
15		raleq 2505	. . . . . . 7 |- ( u = ( w u. { z } ) -> ( A. x e. u ps <-> A. x e. ( w u. { z } ) ps ) )
16	14, 15	anbi12d 442	. . . . . 6 |- ( u = ( w u. { z } ) -> ( ( f : u --> B /\ A. x e. u ps ) <-> ( f : ( w u. { z } ) --> B /\ A. x e. ( w u. { z } ) ps ) ) )
17	16	exbidv 1706	. . . . 5 |- ( u = ( w u. { z } ) -> ( E. f ( f : u --> B /\ A. x e. u ps ) <-> E. f ( f : ( w u. { z } ) --> B /\ A. x e. ( w u. { z } ) ps ) ) )
18		feq1 5030	. . . . . . 7 |- ( f = g -> ( f : ( w u. { z } ) --> B <-> g : ( w u. { z } ) --> B ) )
19		vex 2560	. . . . . . . . . . 11 |- f e. _V
20		vex 2560	. . . . . . . . . . 11 |- x e. _V
21	19, 20	fvex 5195	. . . . . . . . . 10 |- ( f ` x ) e. _V
22		ac6sfi.1	. . . . . . . . . 10 |- ( y = ( f ` x ) -> ( ph <-> ps ) )
23	21, 22	sbcie 2797	. . . . . . . . 9 |- ( [. ( f ` x ) / y ]. ph <-> ps )
24		fveq1 5177	. . . . . . . . . 10 |- ( f = g -> ( f ` x ) = ( g ` x ) )
25	24	sbceq1d 2769	. . . . . . . . 9 |- ( f = g -> ( [. ( f ` x ) / y ]. ph <-> [. ( g ` x ) / y ]. ph ) )
26	23, 25	syl5bbr 183	. . . . . . . 8 |- ( f = g -> ( ps <-> [. ( g ` x ) / y ]. ph ) )
27	26	ralbidv 2326	. . . . . . 7 |- ( f = g -> ( A. x e. ( w u. { z } ) ps <-> A. x e. ( w u. { z } ) [. ( g ` x ) / y ]. ph ) )
28	18, 27	anbi12d 442	. . . . . 6 |- ( f = g -> ( ( f : ( w u. { z } ) --> B /\ A. x e. ( w u. { z } ) ps ) <-> ( g : ( w u. { z } ) --> B /\ A. x e. ( w u. { z } ) [. ( g ` x ) / y ]. ph ) ) )
29	28	cbvexv 1795	. . . . 5 |- ( E. f ( f : ( w u. { z } ) --> B /\ A. x e. ( w u. { z } ) ps ) <-> E. g ( g : ( w u. { z } ) --> B /\ A. x e. ( w u. { z } ) [. ( g ` x ) / y ]. ph ) )
30	17, 29	syl6bb 185	. . . 4 |- ( u = ( w u. { z } ) -> ( E. f ( f : u --> B /\ A. x e. u ps ) <-> E. g ( g : ( w u. { z } ) --> B /\ A. x e. ( w u. { z } ) [. ( g ` x ) / y ]. ph ) ) )
31	13, 30	imbi12d 223	. . 3 |- ( u = ( w u. { z } ) -> ( ( A. x e. u E. y e. B ph -> E. f ( f : u --> B /\ A. x e. u ps ) ) <-> ( A. x e. ( w u. { z } ) E. y e. B ph -> E. g ( g : ( w u. { z } ) --> B /\ A. x e. ( w u. { z } ) [. ( g ` x ) / y ]. ph ) ) ) )
32		raleq 2505	. . . 4 |- ( u = A -> ( A. x e. u E. y e. B ph <-> A. x e. A E. y e. B ph ) )
33		feq2 5031	. . . . . 6 |- ( u = A -> ( f : u --> B <-> f : A --> B ) )
34		raleq 2505	. . . . . 6 |- ( u = A -> ( A. x e. u ps <-> A. x e. A ps ) )
35	33, 34	anbi12d 442	. . . . 5 |- ( u = A -> ( ( f : u --> B /\ A. x e. u ps ) <-> ( f : A --> B /\ A. x e. A ps ) ) )
36	35	exbidv 1706	. . . 4 |- ( u = A -> ( E. f ( f : u --> B /\ A. x e. u ps ) <-> E. f ( f : A --> B /\ A. x e. A ps ) ) )
37	32, 36	imbi12d 223	. . 3 |- ( u = A -> ( ( A. x e. u E. y e. B ph -> E. f ( f : u --> B /\ A. x e. u ps ) ) <-> ( A. x e. A E. y e. B ph -> E. f ( f : A --> B /\ A. x e. A ps ) ) ) )
38		f0 5080	. . . 4 |- (/) : (/) --> B
39		0ex 3884	. . . . 5 |- (/) e. _V
40		ral0 3322	. . . . . . 7 |- A. x e. (/) ps
41	40	biantru 286	. . . . . 6 |- ( f : (/) --> B <-> ( f : (/) --> B /\ A. x e. (/) ps ) )
42		feq1 5030	. . . . . 6 |- ( f = (/) -> ( f : (/) --> B <-> (/) : (/) --> B ) )
43	41, 42	syl5bbr 183	. . . . 5 |- ( f = (/) -> ( ( f : (/) --> B /\ A. x e. (/) ps ) <-> (/) : (/) --> B ) )
44	39, 43	spcev 2647	. . . 4 |- ( (/) : (/) --> B -> E. f ( f : (/) --> B /\ A. x e. (/) ps ) )
45	38, 44	mp1i 10	. . 3 |- ( A. x e. (/) E. y e. B ph -> E. f ( f : (/) --> B /\ A. x e. (/) ps ) )
46		ssun1 3106	. . . . . . 7 |- w C_ ( w u. { z } )
47		ssralv 3004	. . . . . . 7 |- ( w C_ ( w u. { z } ) -> ( A. x e. ( w u. { z } ) E. y e. B ph -> A. x e. w E. y e. B ph ) )
48	46, 47	ax-mp 7	. . . . . 6 |- ( A. x e. ( w u. { z } ) E. y e. B ph -> A. x e. w E. y e. B ph )
49	48	imim1i 54	. . . . 5 |- ( ( A. x e. w E. y e. B ph -> E. f ( f : w --> B /\ A. x e. w ps ) ) -> ( A. x e. ( w u. { z } ) E. y e. B ph -> E. f ( f : w --> B /\ A. x e. w ps ) ) )
50		ssun2 3107	. . . . . . . . 9 |- { z } C_ ( w u. { z } )
51		ssralv 3004	. . . . . . . . 9 |- ( { z } C_ ( w u. { z } ) -> ( A. x e. ( w u. { z } ) E. y e. B ph -> A. x e. { z } E. y e. B ph ) )
52	50, 51	ax-mp 7	. . . . . . . 8 |- ( A. x e. ( w u. { z } ) E. y e. B ph -> A. x e. { z } E. y e. B ph )
53		vex 2560	. . . . . . . . . 10 |- z e. _V
54		ralsnsg 3407	. . . . . . . . . 10 |- ( z e. _V -> ( A. x e. { z } E. y e. B ph <-> [. z / x ]. E. y e. B ph ) )
55	53, 54	ax-mp 7	. . . . . . . . 9 |- ( A. x e. { z } E. y e. B ph <-> [. z / x ]. E. y e. B ph )
56		sbcrex 2837	. . . . . . . . 9 |- ( [. z / x ]. E. y e. B ph <-> E. y e. B [. z / x ]. ph )
57	55, 56	bitri 173	. . . . . . . 8 |- ( A. x e. { z } E. y e. B ph <-> E. y e. B [. z / x ]. ph )
58	52, 57	sylib 127	. . . . . . 7 |- ( A. x e. ( w u. { z } ) E. y e. B ph -> E. y e. B [. z / x ]. ph )
59		nfv 1421	. . . . . . . 8 |- F/ y -. z e. w
60		nfv 1421	. . . . . . . . 9 |- F/ y E. f ( f : w --> B /\ A. x e. w ps )
61		nfv 1421	. . . . . . . . . . 11 |- F/ y g : ( w u. { z } ) --> B
62		nfcv 2178	. . . . . . . . . . . 12 |- F/_ y ( w u. { z } )
63		nfsbc1v 2782	. . . . . . . . . . . 12 |- F/ y [. ( g ` x ) / y ]. ph
64	62, 63	nfralxy 2360	. . . . . . . . . . 11 |- F/ y A. x e. ( w u. { z } ) [. ( g ` x ) / y ]. ph
65	61, 64	nfan 1457	. . . . . . . . . 10 |- F/ y ( g : ( w u. { z } ) --> B /\ A. x e. ( w u. { z } ) [. ( g ` x ) / y ]. ph )
66	65	nfex 1528	. . . . . . . . 9 |- F/ y E. g ( g : ( w u. { z } ) --> B /\ A. x e. ( w u. { z } ) [. ( g ` x ) / y ]. ph )
67	60, 66	nfim 1464	. . . . . . . 8 |- F/ y ( E. f ( f : w --> B /\ A. x e. w ps ) -> E. g ( g : ( w u. { z } ) --> B /\ A. x e. ( w u. { z } ) [. ( g ` x ) / y ]. ph ) )
68		simprl 483	. . . . . . . . . . . . 13 |- ( ( ( -. z e. w /\ y e. B /\ [. z / x ]. ph ) /\ ( f : w --> B /\ A. x e. w ps ) ) -> f : w --> B )
69		vex 2560	. . . . . . . . . . . . . . . 16 |- y e. _V
70	53, 69	f1osn 5166	. . . . . . . . . . . . . . 15 |- { <. z , y >. } : { z } -1-1-onto-> { y }
71		f1of 5126	. . . . . . . . . . . . . . 15 |- ( { <. z , y >. } : { z } -1-1-onto-> { y } -> { <. z , y >. } : { z } --> { y } )
72	70, 71	mp1i 10	. . . . . . . . . . . . . 14 |- ( ( ( -. z e. w /\ y e. B /\ [. z / x ]. ph ) /\ ( f : w --> B /\ A. x e. w ps ) ) -> { <. z , y >. } : { z } --> { y } )
73		simpl2 908	. . . . . . . . . . . . . . 15 |- ( ( ( -. z e. w /\ y e. B /\ [. z / x ]. ph ) /\ ( f : w --> B /\ A. x e. w ps ) ) -> y e. B )
74	73	snssd 3509	. . . . . . . . . . . . . 14 |- ( ( ( -. z e. w /\ y e. B /\ [. z / x ]. ph ) /\ ( f : w --> B /\ A. x e. w ps ) ) -> { y } C_ B )
75	72, 74	fssd 5055	. . . . . . . . . . . . 13 |- ( ( ( -. z e. w /\ y e. B /\ [. z / x ]. ph ) /\ ( f : w --> B /\ A. x e. w ps ) ) -> { <. z , y >. } : { z } --> B )
76		simpl1 907	. . . . . . . . . . . . . 14 |- ( ( ( -. z e. w /\ y e. B /\ [. z / x ]. ph ) /\ ( f : w --> B /\ A. x e. w ps ) ) -> -. z e. w )
77		disjsn 3432	. . . . . . . . . . . . . 14 |- ( ( w i^i { z } ) = (/) <-> -. z e. w )
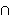
78	76, 77	sylibr 137	. . . . . . . . . . . . 13 |- ( ( ( -. z e. w /\ y e. B /\ [. z / x ]. ph ) /\ ( f : w --> B /\ A. x e. w ps ) ) -> ( w i^i { z } ) = (/) )
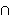79		fun2 5064	. . . . . . . . . . . . 13 |- ( ( ( f : w --> B /\ { <. z , y >. } : { z } --> B ) /\ ( w i^i { z } ) = (/) ) -> ( f u. { <. z , y >. } ) : ( w u. { z } ) --> B )
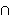80	68, 75, 78, 79	syl21anc 1134	. . . . . . . . . . . 12 |- ( ( ( -. z e. w /\ y e. B /\ [. z / x ]. ph ) /\ ( f : w --> B /\ A. x e. w ps ) ) -> ( f u. { <. z , y >. } ) : ( w u. { z } ) --> B )
81		simprr 484	. . . . . . . . . . . . . 14 |- ( ( ( -. z e. w /\ y e. B /\ [. z / x ]. ph ) /\ ( f : w --> B /\ A. x e. w ps ) ) -> A. x e. w ps )
82		eleq1a 2109	. . . . . . . . . . . . . . . . . . 19 |- ( x e. w -> ( z = x -> z e. w ) )
83	82	necon3bd 2248	. . . . . . . . . . . . . . . . . 18 |- ( x e. w -> ( -. z e. w -> z =/= x ) )
84	83	impcom 116	. . . . . . . . . . . . . . . . 17 |- ( ( -. z e. w /\ x e. w ) -> z =/= x )
85		fvunsng 5357	. . . . . . . . . . . . . . . . . 18 |- ( ( x e. _V /\ z =/= x ) -> ( ( f u. { <. z , y >. } ) ` x ) = ( f ` x ) )
86	20, 85	mpan 400	. . . . . . . . . . . . . . . . 17 |- ( z =/= x -> ( ( f u. { <. z , y >. } ) ` x ) = ( f ` x ) )
87		dfsbcq 2766	. . . . . . . . . . . . . . . . . 18 |- ( ( ( f u. { <. z , y >. } ) ` x ) = ( f ` x ) -> ( [. ( ( f u. { <. z , y >. } ) ` x ) / y ]. ph <-> [. ( f ` x ) / y ]. ph ) )
88	87, 23	syl6rbb 186	. . . . . . . . . . . . . . . . 17 |- ( ( ( f u. { <. z , y >. } ) ` x ) = ( f ` x ) -> ( ps <-> [. ( ( f u. { <. z , y >. } ) ` x ) / y ]. ph ) )
89	84, 86, 88	3syl 17	. . . . . . . . . . . . . . . 16 |- ( ( -. z e. w /\ x e. w ) -> ( ps <-> [. ( ( f u. { <. z , y >. } ) ` x ) / y ]. ph ) )
90	89	ralbidva 2322	. . . . . . . . . . . . . . 15 |- ( -. z e. w -> ( A. x e. w ps <-> A. x e. w [. ( ( f u. { <. z , y >. } ) ` x ) / y ]. ph ) )
91	76, 90	syl 14	. . . . . . . . . . . . . 14 |- ( ( ( -. z e. w /\ y e. B /\ [. z / x ]. ph ) /\ ( f : w --> B /\ A. x e. w ps ) ) -> ( A. x e. w ps <-> A. x e. w [. ( ( f u. { <. z , y >. } ) ` x ) / y ]. ph ) )
92	81, 91	mpbid 135	. . . . . . . . . . . . 13 |- ( ( ( -. z e. w /\ y e. B /\ [. z / x ]. ph ) /\ ( f : w --> B /\ A. x e. w ps ) ) -> A. x e. w [. ( ( f u. { <. z , y >. } ) ` x ) / y ]. ph )
93		simpl3 909	. . . . . . . . . . . . . 14 |- ( ( ( -. z e. w /\ y e. B /\ [. z / x ]. ph ) /\ ( f : w --> B /\ A. x e. w ps ) ) -> [. z / x ]. ph )
94		ffun 5048	. . . . . . . . . . . . . . . . 17 |- ( ( f u. { <. z , y >. } ) : ( w u. { z } ) --> B -> Fun ( f u. { <. z , y >. } ) )
95		ssun2 3107	. . . . . . . . . . . . . . . . . 18 |- { <. z , y >. } C_ ( f u. { <. z , y >. } )
96		vsnid 3403	. . . . . . . . . . . . . . . . . . 19 |- z e. { z }
97	69	dmsnop 4794	. . . . . . . . . . . . . . . . . . 19 |- dom { <. z , y >. } = { z }
98	96, 97	eleqtrri 2113	. . . . . . . . . . . . . . . . . 18 |- z e. dom { <. z , y >. }
99		funssfv 5199	. . . . . . . . . . . . . . . . . 18 |- ( ( Fun ( f u. { <. z , y >. } ) /\ { <. z , y >. } C_ ( f u. { <. z , y >. } ) /\ z e. dom { <. z , y >. } ) -> ( ( f u. { <. z , y >. } ) ` z ) = ( { <. z , y >. } ` z ) )
100	95, 98, 99	mp3an23 1224	. . . . . . . . . . . . . . . . 17 |- ( Fun ( f u. { <. z , y >. } ) -> ( ( f u. { <. z , y >. } ) ` z ) = ( { <. z , y >. } ` z ) )
101	80, 94, 100	3syl 17	. . . . . . . . . . . . . . . 16 |- ( ( ( -. z e. w /\ y e. B /\ [. z / x ]. ph ) /\ ( f : w --> B /\ A. x e. w ps ) ) -> ( ( f u. { <. z , y >. } ) ` z ) = ( { <. z , y >. } ` z ) )
102	53, 69	fvsn 5358	. . . . . . . . . . . . . . . 16 |- ( { <. z , y >. } ` z ) = y
103	101, 102	syl6req 2089	. . . . . . . . . . . . . . 15 |- ( ( ( -. z e. w /\ y e. B /\ [. z / x ]. ph ) /\ ( f : w --> B /\ A. x e. w ps ) ) -> y = ( ( f u. { <. z , y >. } ) ` z ) )
104		ralsnsg 3407	. . . . . . . . . . . . . . . . 17 |- ( z e. _V -> ( A. x e. { z } ph <-> [. z / x ]. ph ) )
105	53, 104	ax-mp 7	. . . . . . . . . . . . . . . 16 |- ( A. x e. { z } ph <-> [. z / x ]. ph )
106		elsni 3393	. . . . . . . . . . . . . . . . . . . . 21 |- ( x e. { z } -> x = z )
107	106	fveq2d 5182	. . . . . . . . . . . . . . . . . . . 20 |- ( x e. { z } -> ( ( f u. { <. z , y >. } ) ` x ) = ( ( f u. { <. z , y >. } ) ` z ) )
108	107	eqeq2d 2051	. . . . . . . . . . . . . . . . . . 19 |- ( x e. { z } -> ( y = ( ( f u. { <. z , y >. } ) ` x ) <-> y = ( ( f u. { <. z , y >. } ) ` z ) ) )
109	108	biimparc 283	. . . . . . . . . . . . . . . . . 18 |- ( ( y = ( ( f u. { <. z , y >. } ) ` z ) /\ x e. { z } ) -> y = ( ( f u. { <. z , y >. } ) ` x ) )
110		sbceq1a 2773	. . . . . . . . . . . . . . . . . 18 |- ( y = ( ( f u. { <. z , y >. } ) ` x ) -> ( ph <-> [. ( ( f u. { <. z , y >. } ) ` x ) / y ]. ph ) )
111	109, 110	syl 14	. . . . . . . . . . . . . . . . 17 |- ( ( y = ( ( f u. { <. z , y >. } ) ` z ) /\ x e. { z } ) -> ( ph <-> [. ( ( f u. { <. z , y >. } ) ` x ) / y ]. ph ) )
112	111	ralbidva 2322	. . . . . . . . . . . . . . . 16 |- ( y = ( ( f u. { <. z , y >. } ) ` z ) -> ( A. x e. { z } ph <-> A. x e. { z } [. ( ( f u. { <. z , y >. } ) ` x ) / y ]. ph ) )
113	105, 112	syl5bbr 183	. . . . . . . . . . . . . . 15 |- ( y = ( ( f u. { <. z , y >. } ) ` z ) -> ( [. z / x ]. ph <-> A. x e. { z } [. ( ( f u. { <. z , y >. } ) ` x ) / y ]. ph ) )
114	103, 113	syl 14	. . . . . . . . . . . . . 14 |- ( ( ( -. z e. w /\ y e. B /\ [. z / x ]. ph ) /\ ( f : w --> B /\ A. x e. w ps ) ) -> ( [. z / x ]. ph <-> A. x e. { z } [. ( ( f u. { <. z , y >. } ) ` x ) / y ]. ph ) )
115	93, 114	mpbid 135	. . . . . . . . . . . . 13 |- ( ( ( -. z e. w /\ y e. B /\ [. z / x ]. ph ) /\ ( f : w --> B /\ A. x e. w ps ) ) -> A. x e. { z } [. ( ( f u. { <. z , y >. } ) ` x ) / y ]. ph )
116		ralun 3125	. . . . . . . . . . . . 13 |- ( ( A. x e. w [. ( ( f u. { <. z , y >. } ) ` x ) / y ]. ph /\ A. x e. { z } [. ( ( f u. { <. z , y >. } ) ` x ) / y ]. ph ) -> A. x e. ( w u. { z } ) [. ( ( f u. { <. z , y >. } ) ` x ) / y ]. ph )
117	92, 115, 116	syl2anc 391	. . . . . . . . . . . 12 |- ( ( ( -. z e. w /\ y e. B /\ [. z / x ]. ph ) /\ ( f : w --> B /\ A. x e. w ps ) ) -> A. x e. ( w u. { z } ) [. ( ( f u. { <. z , y >. } ) ` x ) / y ]. ph )
118	53, 69	opex 3966	. . . . . . . . . . . . . . 15 |- <. z , y >. e. _V
119	118	snex 3937	. . . . . . . . . . . . . 14 |- { <. z , y >. } e. _V
120	19, 119	unex 4176	. . . . . . . . . . . . 13 |- ( f u. { <. z , y >. } ) e. _V
121		feq1 5030	. . . . . . . . . . . . . 14 |- ( g = ( f u. { <. z , y >. } ) -> ( g : ( w u. { z } ) --> B <-> ( f u. { <. z , y >. } ) : ( w u. { z } ) --> B ) )
122		fveq1 5177	. . . . . . . . . . . . . . . 16 |- ( g = ( f u. { <. z , y >. } ) -> ( g ` x ) = ( ( f u. { <. z , y >. } ) ` x ) )
123	122	sbceq1d 2769	. . . . . . . . . . . . . . 15 |- ( g = ( f u. { <. z , y >. } ) -> ( [. ( g ` x ) / y ]. ph <-> [. ( ( f u. { <. z , y >. } ) ` x ) / y ]. ph ) )
124	123	ralbidv 2326	. . . . . . . . . . . . . 14 |- ( g = ( f u. { <. z , y >. } ) -> ( A. x e. ( w u. { z } ) [. ( g ` x ) / y ]. ph <-> A. x e. ( w u. { z } ) [. ( ( f u. { <. z , y >. } ) ` x ) / y ]. ph ) )
125	121, 124	anbi12d 442	. . . . . . . . . . . . 13 |- ( g = ( f u. { <. z , y >. } ) -> ( ( g : ( w u. { z } ) --> B /\ A. x e. ( w u. { z } ) [. ( g ` x ) / y ]. ph ) <-> ( ( f u. { <. z , y >. } ) : ( w u. { z } ) --> B /\ A. x e. ( w u. { z } ) [. ( ( f u. { <. z , y >. } ) ` x ) / y ]. ph ) ) )
126	120, 125	spcev 2647	. . . . . . . . . . . 12 |- ( ( ( f u. { <. z , y >. } ) : ( w u. { z } ) --> B /\ A. x e. ( w u. { z } ) [. ( ( f u. { <. z , y >. } ) ` x ) / y ]. ph ) -> E. g ( g : ( w u. { z } ) --> B /\ A. x e. ( w u. { z } ) [. ( g ` x ) / y ]. ph ) )
127	80, 117, 126	syl2anc 391	. . . . . . . . . . 11 |- ( ( ( -. z e. w /\ y e. B /\ [. z / x ]. ph ) /\ ( f : w --> B /\ A. x e. w ps ) ) -> E. g ( g : ( w u. { z } ) --> B /\ A. x e. ( w u. { z } ) [. ( g ` x ) / y ]. ph ) )
128	127	ex 108	. . . . . . . . . 10 |- ( ( -. z e. w /\ y e. B /\ [. z / x ]. ph ) -> ( ( f : w --> B /\ A. x e. w ps ) -> E. g ( g : ( w u. { z } ) --> B /\ A. x e. ( w u. { z } ) [. ( g ` x ) / y ]. ph ) ) )
129	128	exlimdv 1700	. . . . . . . . 9 |- ( ( -. z e. w /\ y e. B /\ [. z / x ]. ph ) -> ( E. f ( f : w --> B /\ A. x e. w ps ) -> E. g ( g : ( w u. { z } ) --> B /\ A. x e. ( w u. { z } ) [. ( g ` x ) / y ]. ph ) ) )
130	129	3exp 1103	. . . . . . . 8 |- ( -. z e. w -> ( y e. B -> ( [. z / x ]. ph -> ( E. f ( f : w --> B /\ A. x e. w ps ) -> E. g ( g : ( w u. { z } ) --> B /\ A. x e. ( w u. { z } ) [. ( g ` x ) / y ]. ph ) ) ) ) )
131	59, 67, 130	rexlimd 2430	. . . . . . 7 |- ( -. z e. w -> ( E. y e. B [. z / x ]. ph -> ( E. f ( f : w --> B /\ A. x e. w ps ) -> E. g ( g : ( w u. { z } ) --> B /\ A. x e. ( w u. { z } ) [. ( g ` x ) / y ]. ph ) ) ) )
132	58, 131	syl5 28	. . . . . 6 |- ( -. z e. w -> ( A. x e. ( w u. { z } ) E. y e. B ph -> ( E. f ( f : w --> B /\ A. x e. w ps ) -> E. g ( g : ( w u. { z } ) --> B /\ A. x e. ( w u. { z } ) [. ( g ` x ) / y ]. ph ) ) ) )
133	132	a2d 23	. . . . 5 |- ( -. z e. w -> ( ( A. x e. ( w u. { z } ) E. y e. B ph -> E. f ( f : w --> B /\ A. x e. w ps ) ) -> ( A. x e. ( w u. { z } ) E. y e. B ph -> E. g ( g : ( w u. { z } ) --> B /\ A. x e. ( w u. { z } ) [. ( g ` x ) / y ]. ph ) ) ) )
134	49, 133	syl5 28	. . . 4 |- ( -. z e. w -> ( ( A. x e. w E. y e. B ph -> E. f ( f : w --> B /\ A. x e. w ps ) ) -> ( A. x e. ( w u. { z } ) E. y e. B ph -> E. g ( g : ( w u. { z } ) --> B /\ A. x e. ( w u. { z } ) [. ( g ` x ) / y ]. ph ) ) ) )
135	134	adantl 262	. . 3 |- ( ( w e. Fin /\ -. z e. w ) -> ( ( A. x e. w E. y e. B ph -> E. f ( f : w --> B /\ A. x e. w ps ) ) -> ( A. x e. ( w u. { z } ) E. y e. B ph -> E. g ( g : ( w u. { z } ) --> B /\ A. x e. ( w u. { z } ) [. ( g ` x ) / y ]. ph ) ) ) )
136	6, 12, 31, 37, 45, 135	findcard2s 6347	. 2 |- ( A e. Fin -> ( A. x e. A E. y e. B ph -> E. f ( f : A --> B /\ A. x e. A ps ) ) )
137	136	imp 115	1 |- ( ( A e. Fin /\ A. x e. A E. y e. B ph ) -> E. f ( f : A --> B /\ A. x e. A ps ) )

Syntax hints:   -. wn 3   -> wi 4   /\ wa 97   <-> wb 98   /\ w3a 885   = wceq 1243   E.wex 1381   e. wcel 1393   =/= wne 2204   A.wral 2306   E.wrex 2307   _Vcvv 2557   [.wsbc 2764   u. cun 2915   i^i cin 2916   C_ wss 2917   (/)c0 3224   {csn 3375   <.cop 3378   dom cdm 4345   Fun wfun 4896   -->wf 4898   -1-1-onto->wf1o 4901   ` cfv 4902   Fincfn 6221

This theorem was proved from axioms:  ax-1 5  ax-2 6  ax-mp 7  ax-ia1 99  ax-ia2 100  ax-ia3 101  ax-in1 544  ax-in2 545  ax-io 630  ax-5 1336  ax-7 1337  ax-gen 1338  ax-ie1 1382  ax-ie2 1383  ax-8 1395  ax-10 1396  ax-11 1397  ax-i12 1398  ax-bndl 1399  ax-4 1400  ax-13 1404  ax-14 1405  ax-17 1419  ax-i9 1423  ax-ial 1427  ax-i5r 1428  ax-ext 2022  ax-coll 3872  ax-sep 3875  ax-nul 3883  ax-pow 3927  ax-pr 3944  ax-un 4170  ax-setind 4262  ax-iinf 4311

This theorem depends on definitions:  df-bi 110  df-dc 743  df-3or 886  df-3an 887  df-tru 1246  df-fal 1249  df-nf 1350  df-sb 1646  df-eu 1903  df-mo 1904  df-clab 2027  df-cleq 2033  df-clel 2036  df-nfc 2167  df-ne 2206  df-ral 2311  df-rex 2312  df-reu 2313  df-rab 2315  df-v 2559  df-sbc 2765  df-csb 2853  df-dif 2920  df-un 2922  df-in 2924  df-ss 2931  df-nul 3225  df-if 3332  df-pw 3361  df-sn 3381  df-pr 3382  df-op 3384  df-uni 3581  df-int 3616  df-iun 3659  df-br 3765  df-opab 3819  df-mpt 3820  df-tr 3855  df-id 4030  df-iord 4103  df-on 4105  df-suc 4108  df-iom 4314  df-xp 4351  df-rel 4352  df-cnv 4353  df-co 4354  df-dm 4355  df-rn 4356  df-res 4357  df-ima 4358  df-iota 4867  df-fun 4904  df-fn 4905  df-f 4906  df-f1 4907  df-fo 4908  df-f1o 4909  df-fv 4910  df-er 6106  df-en 6222  df-fin 6224

This theorem is referenced by: (None)