| Description: A context has type
boolean.
This and the next few axioms are not strictly necessary, and are
conservative on any theorem for which every variable has a specified
type, but by adding this axiom we can save some typehood hypotheses in
many theorems. The easy way to see that this axiom is conservative is
to note that every axiom and inference rule that constructs a theorem of
the form 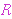 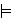  where where 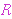 and and  are type variables, also
ensures that are type variables, also
ensures that 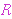 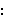 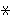 and and  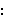 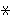 .
Thus it is impossible to
prove any theorem .
Thus it is impossible to
prove any theorem 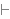 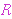 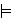  unless both unless both 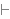 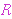 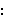 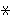 and and
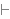  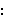 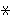 had been previously derived, so it is conservative to
deduce had been previously derived, so it is conservative to
deduce 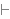 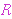 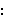 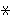 from from 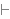
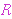 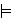  . The same remark applies to
the construction of the theorem . The same remark applies to
the construction of the theorem 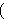   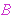 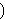 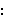 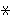 - there is only one
rule that creates a formula of this type, namely wct 44, and
it requires
that - there is only one
rule that creates a formula of this type, namely wct 44, and
it requires
that  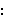 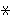 and and 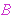 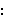 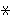 be previously
established, so it is
safe to reverse the process in wctl 31 and wctr 32. be previously
established, so it is
safe to reverse the process in wctl 31 and wctr 32. |